Lanczos interpolation explained

This is a rendered version of the notebook. Head over to the Mathematica file for a version you can actually play with (although you will have to buy Mathematica itself).

The problem, and some solutions

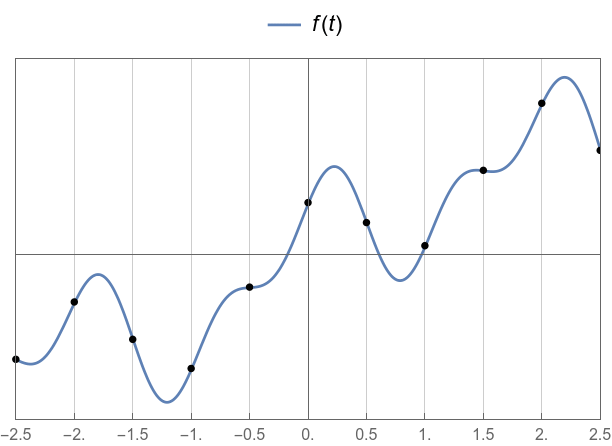
The wobbly example function:

Evenly spaced samples, symmetric about the y axis.

Generate evenly spaced samples for a given expression.

The first example sampled function.

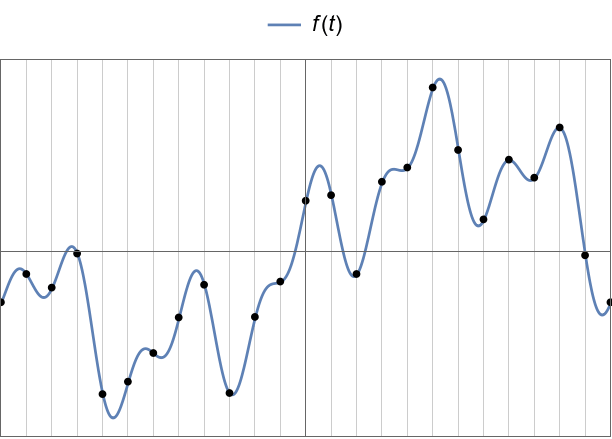
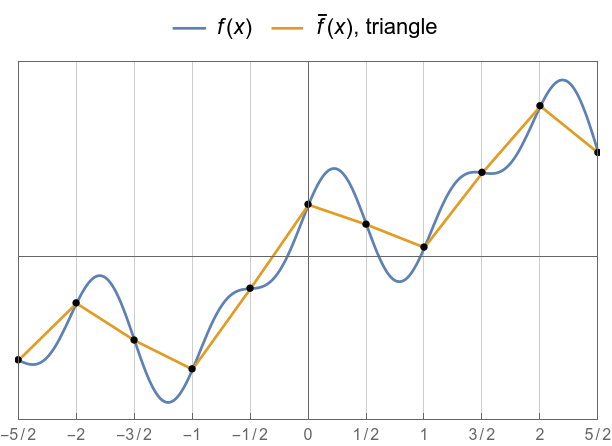
A wrapper to render interpolations nicely (signal in blue, interpolation in gold).

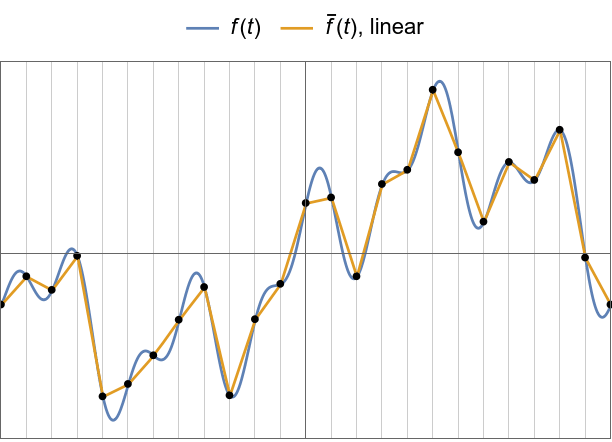
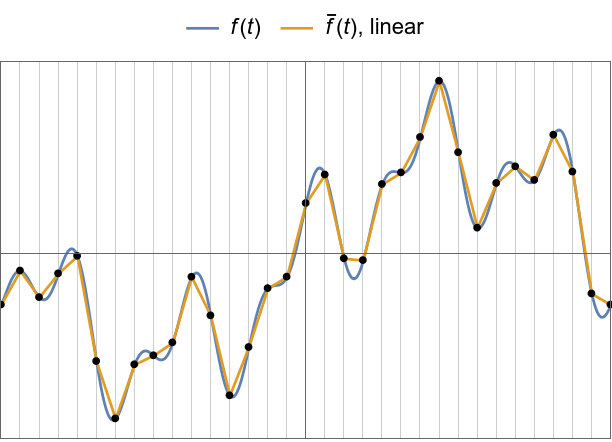
Linear interpolation examples.

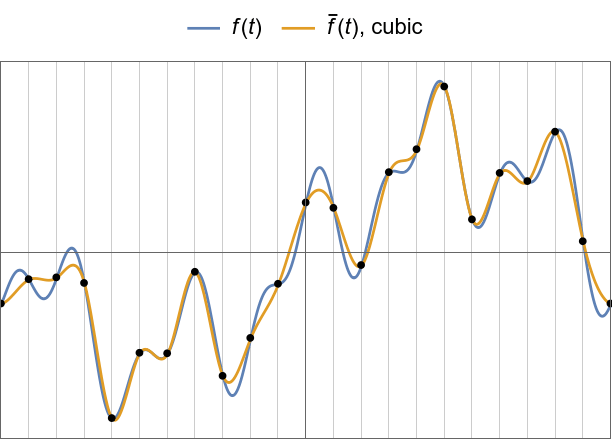
Cubic interpolation example.

Interpolation and convolution

Display fractions on a single line (for higher legibility in legends).

Our sample function, again.

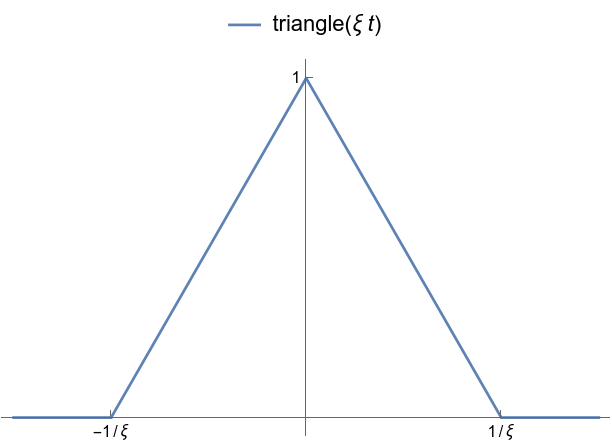
The triangle interpolation function.

Given an interpolation function, a frequency, and a point, stretches it to the frequency, and centers it around the point.

Evaluates and plots a single point using convolution.

Convolve was already taken by Mathematica, and mine is slightly different.

Plots the whole convolution.

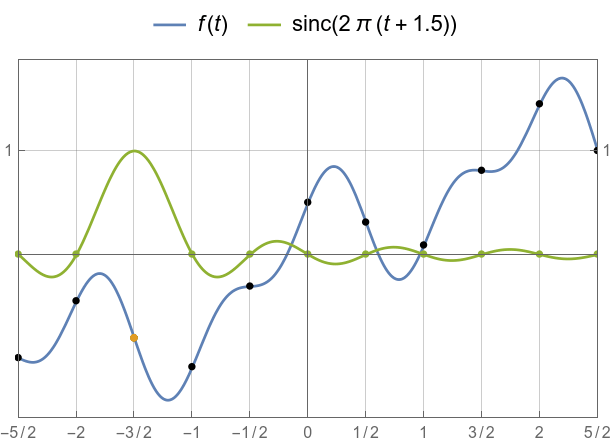
The samples do not change after convolutions (for well behaved interpolation functions).

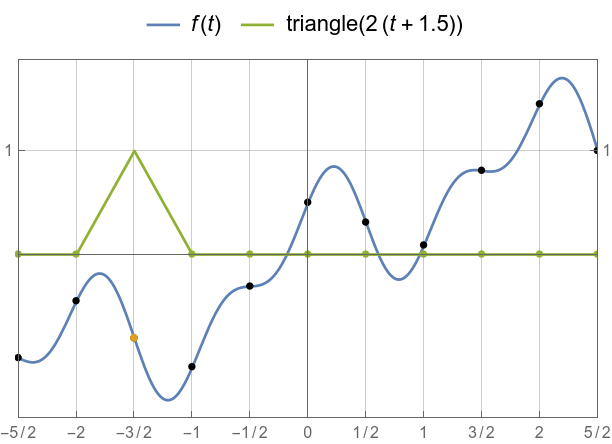
Visual aid for triangle = linear interpolation.

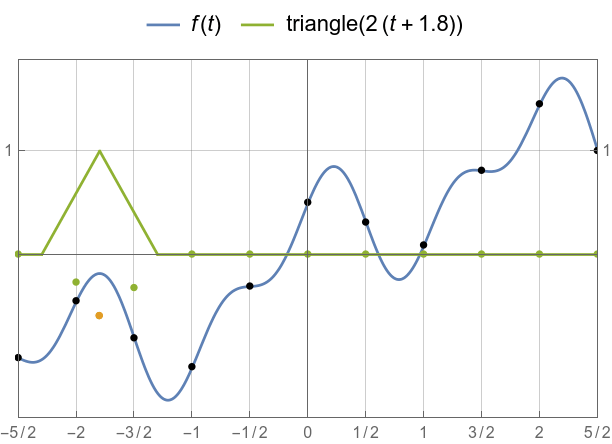
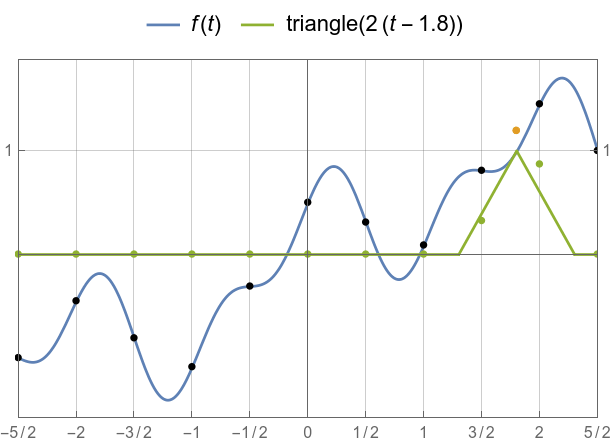
Full linear interpolation through convolution.

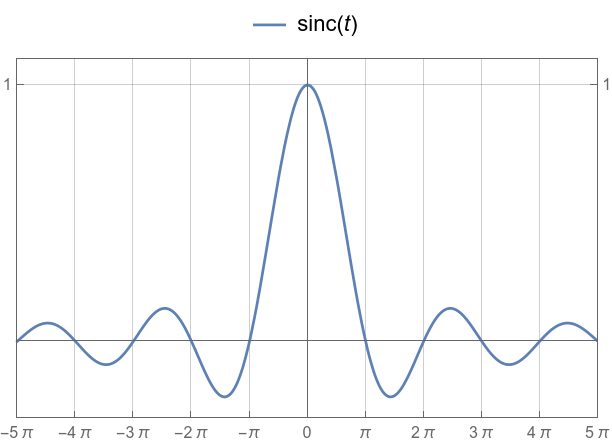
sinc, master interpolator

sinc in all its glory.

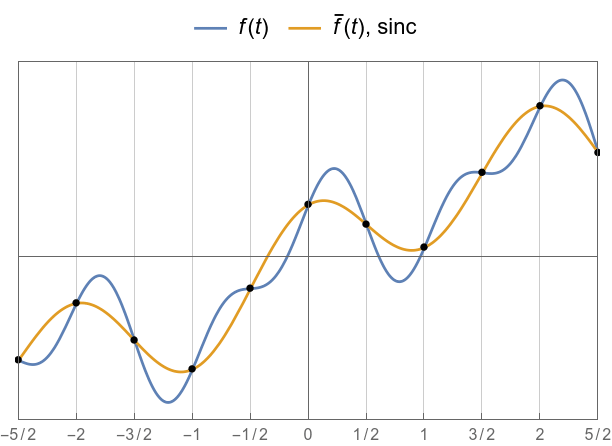
Again, the samples stay put.

But in between, all other samples contribute to the interpolation.

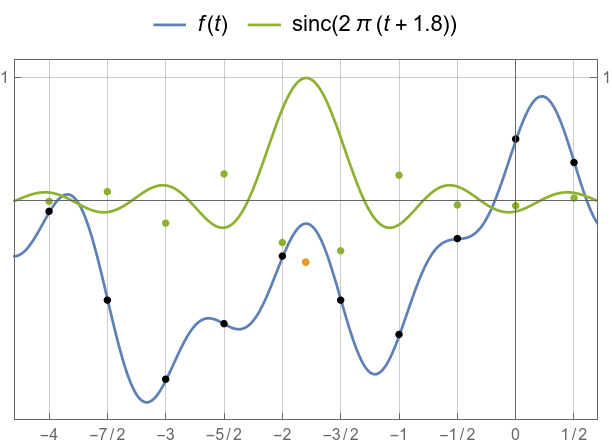
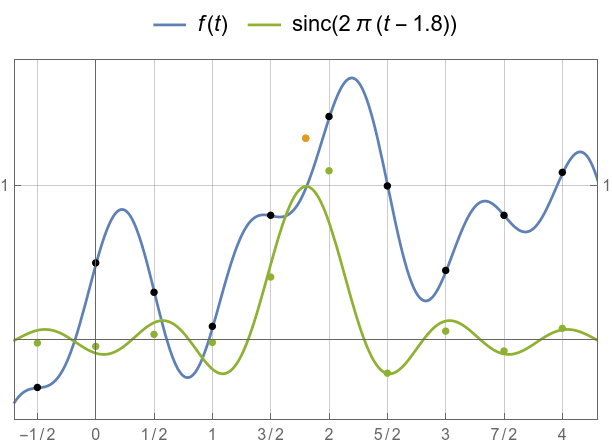
Fourier transform, and inverse.

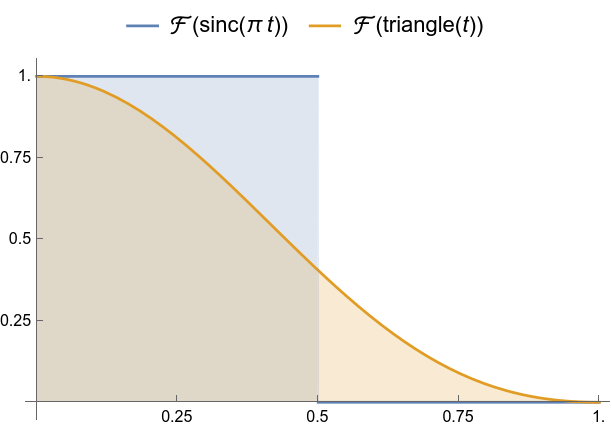
sinc and triangle and their Fourier transforms, compared.

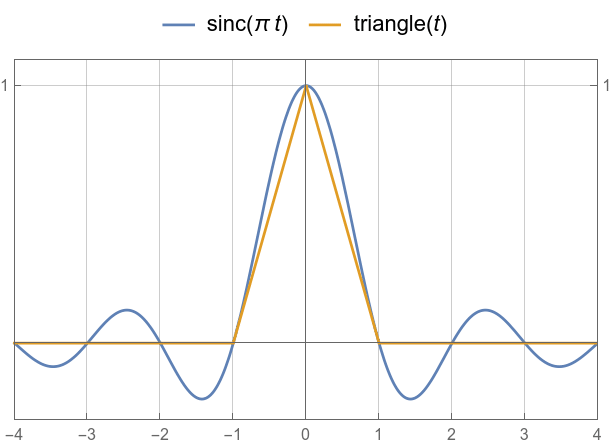
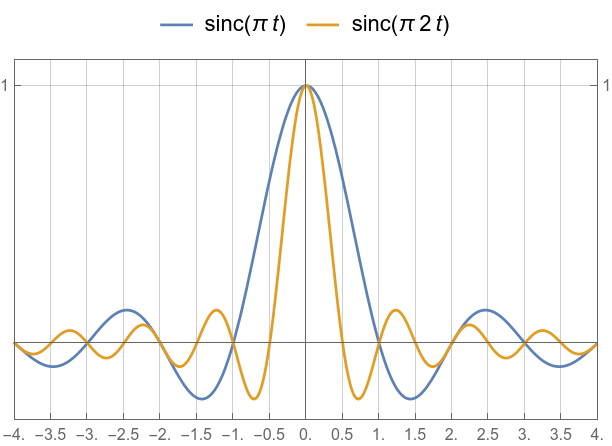
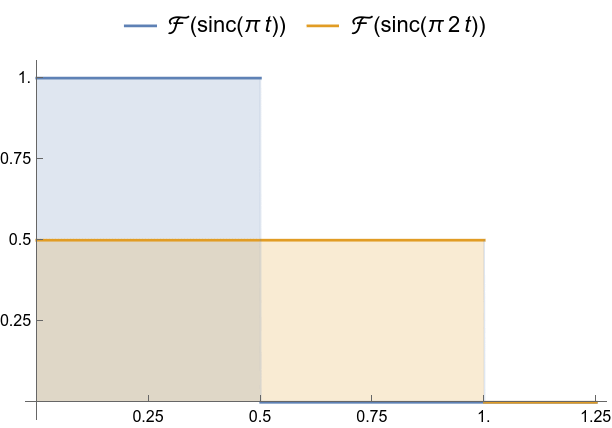
Different width sincs  compared.

Interpolating with sinc — an example

Our original function and its components.

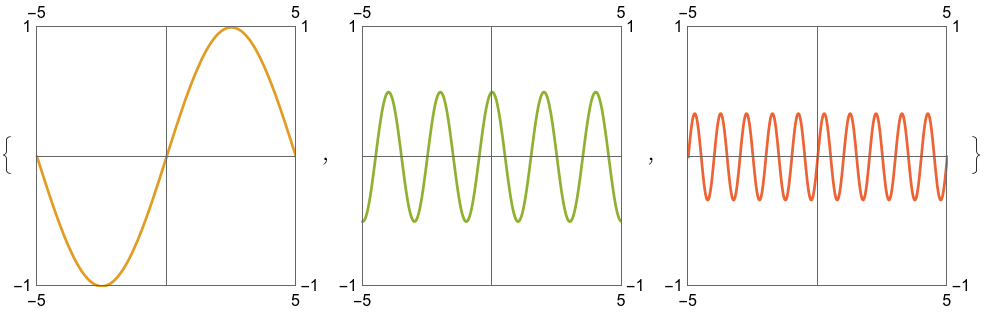
Its Fourier transform, made up of Dirac deltas.

We can’t really plot the Dirac deltas, so let’s do it manually.

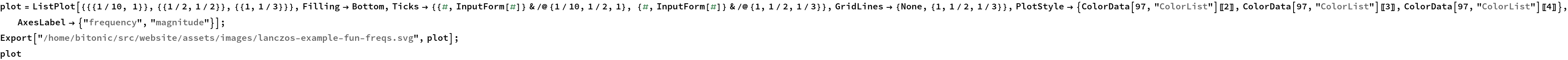
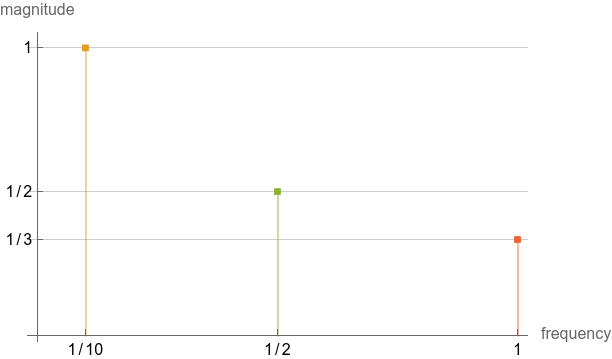
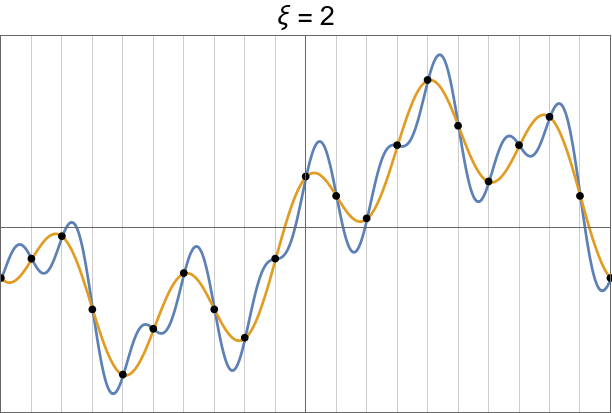
Show how we need to get past the highest-frequency Dirac delta to perfectly reconstruct the signal.

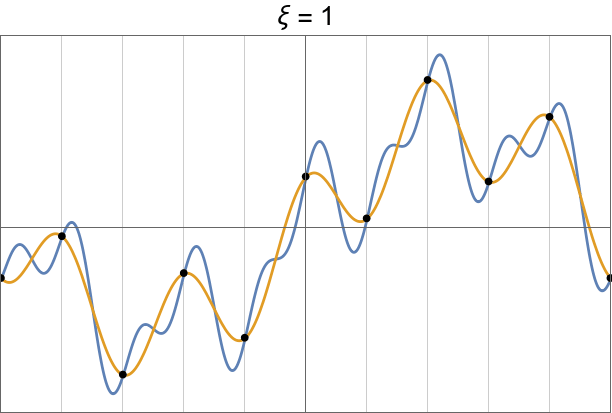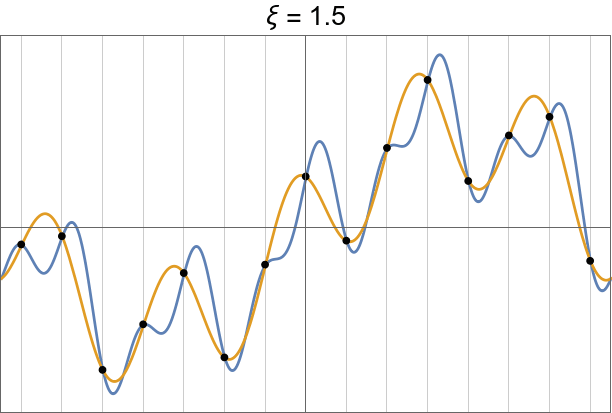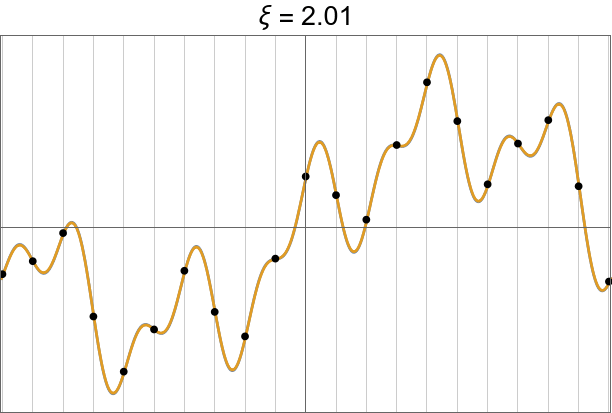The problem with sinc

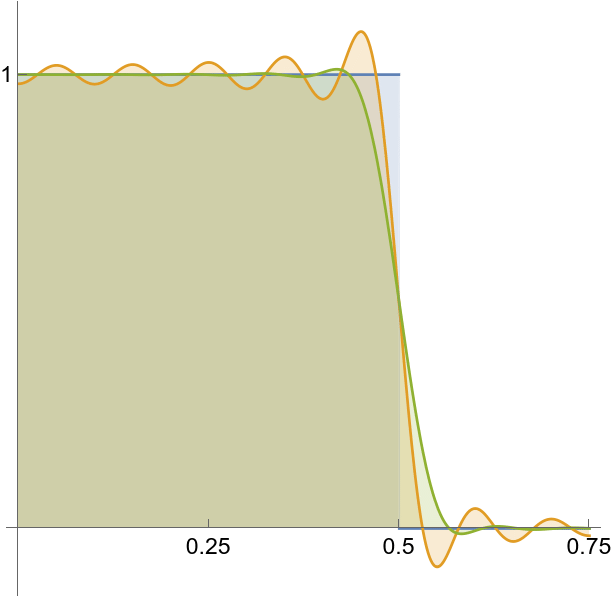
Simple example of a jump discontinuity.

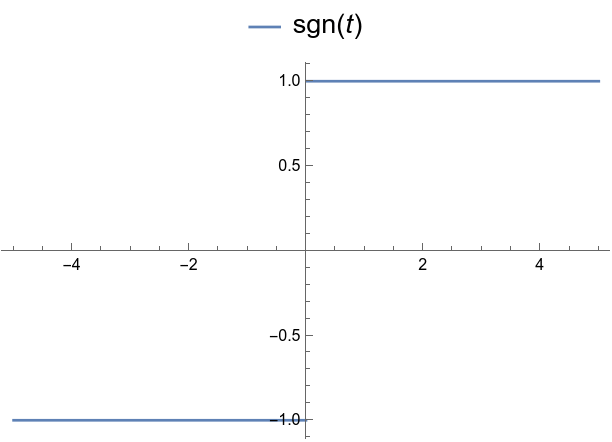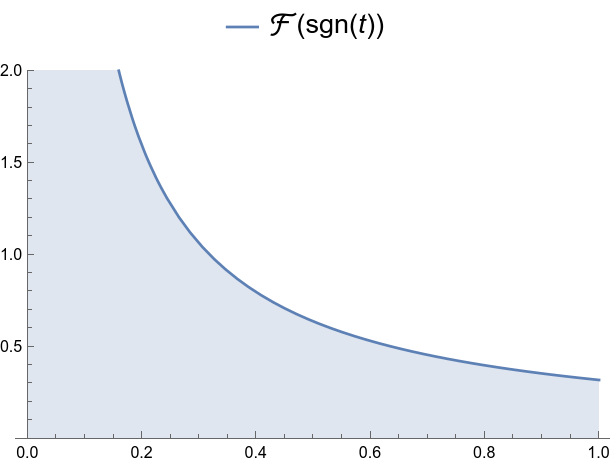Gibbs oscillations.

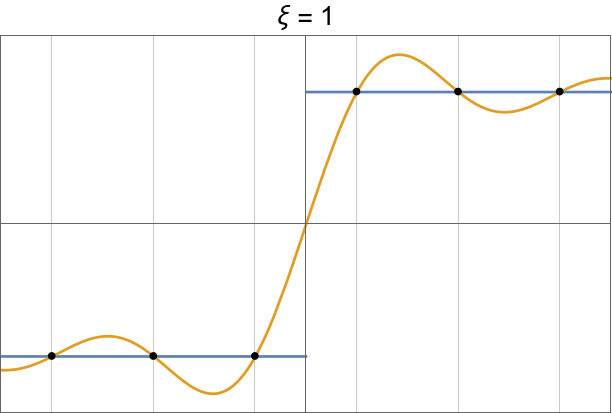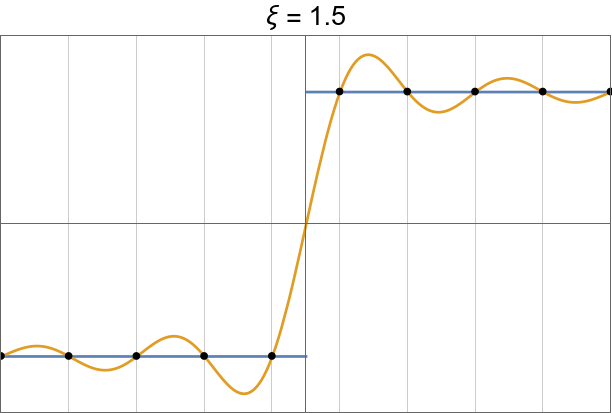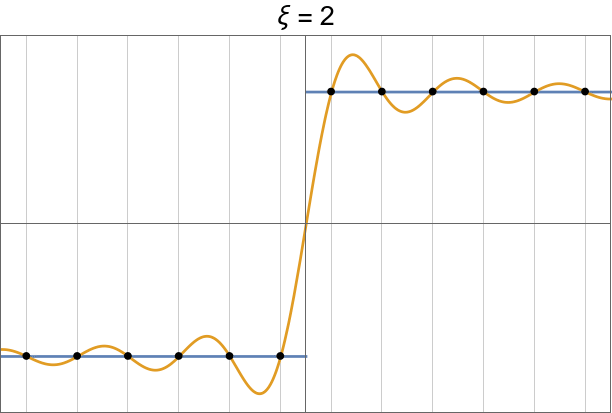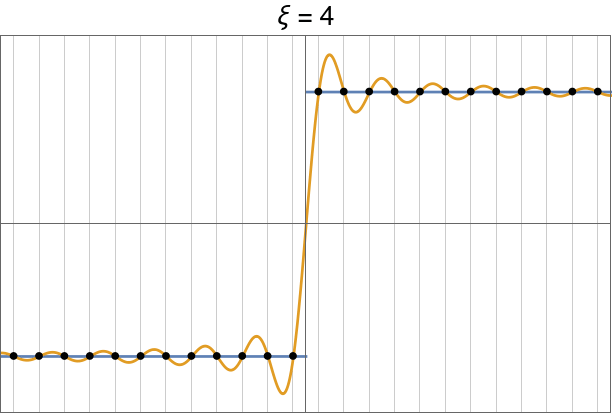sinc -- chopped and screwed

Utility to truncate a function.

And our truncated .

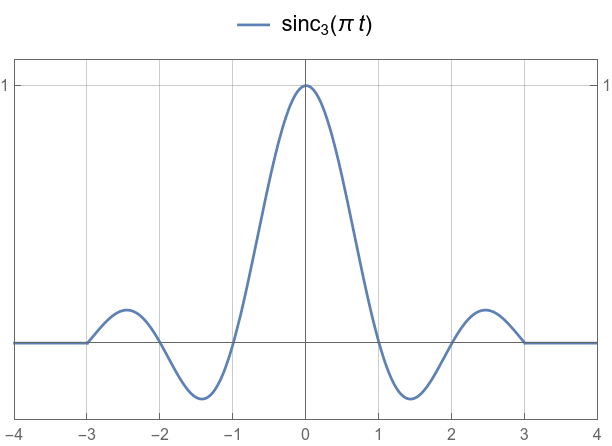
...which doesn’t interpolate so well.

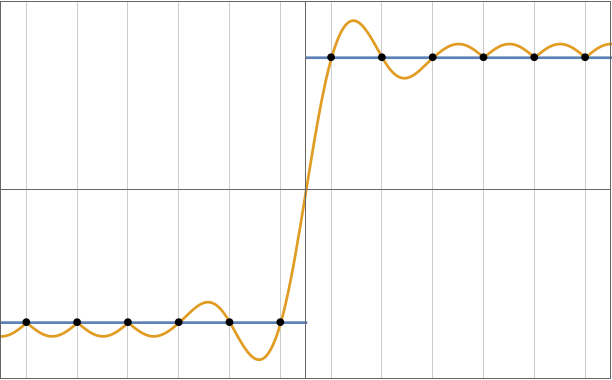
Gibbs oscillations redux -- this time in the spectrum of .

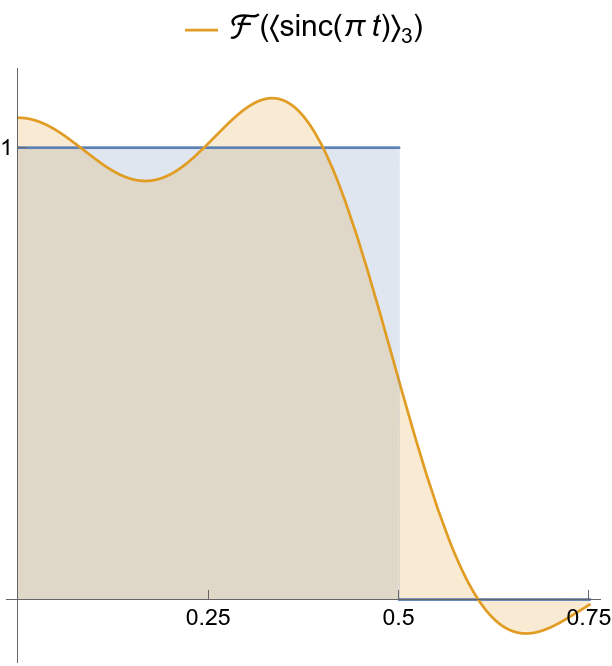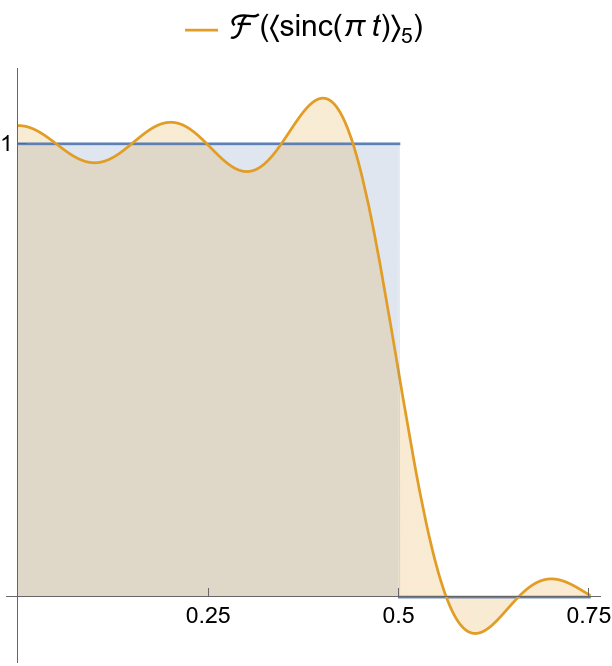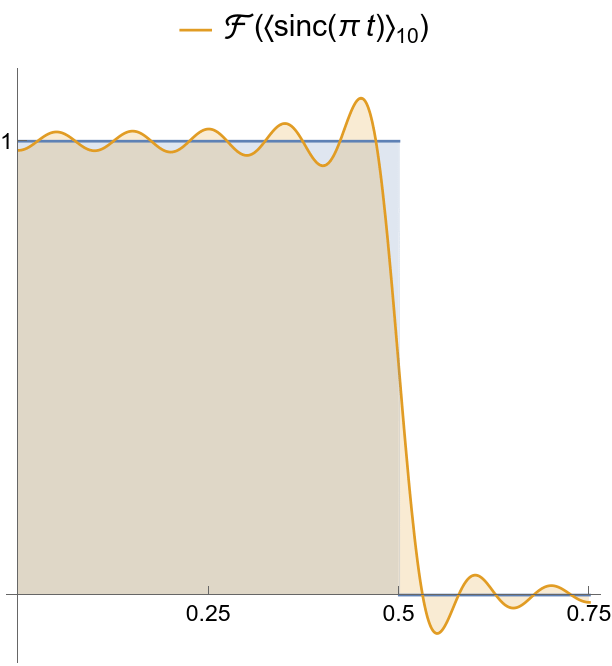Error together with carrier wave.

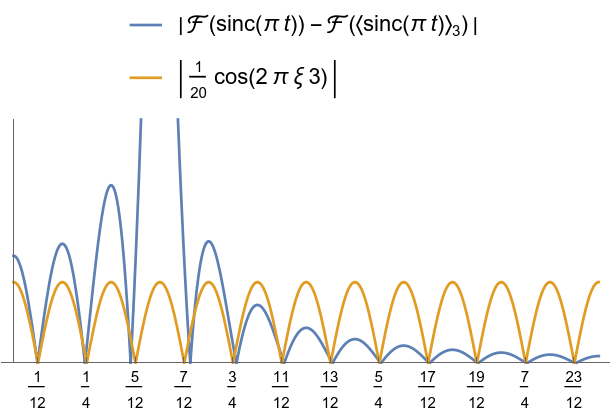
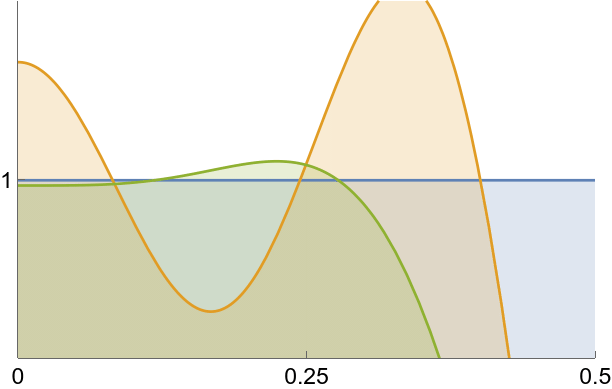
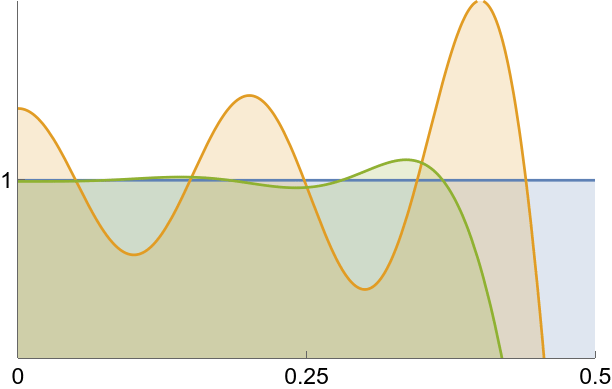
Smoothed spectrum using Lanczos’ method.

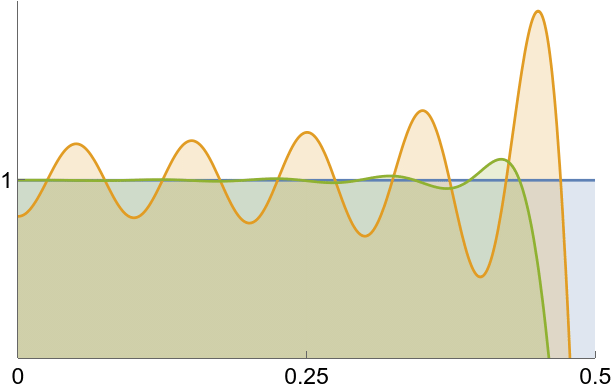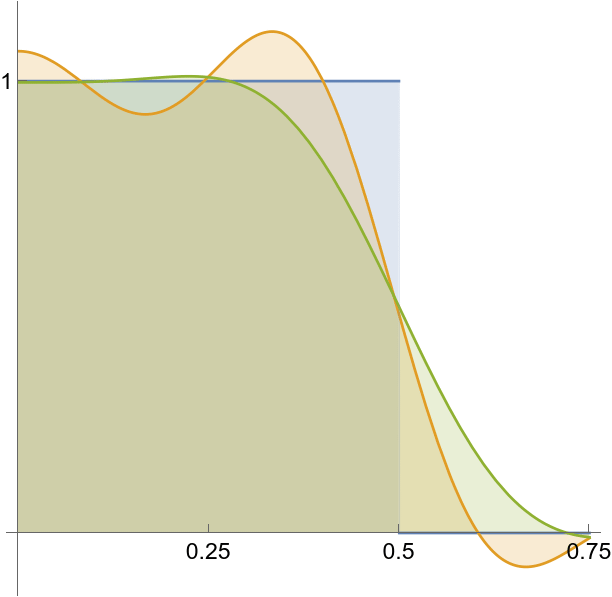
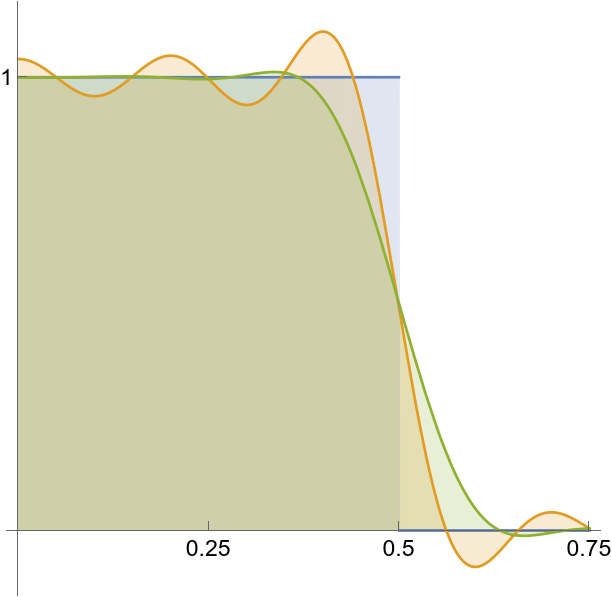
sinc, , and smoothed compared.
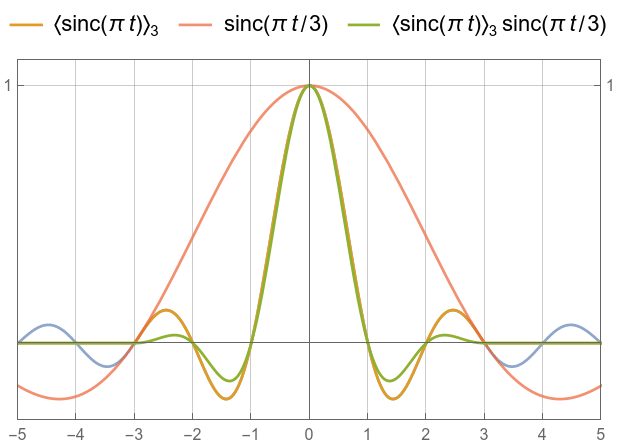
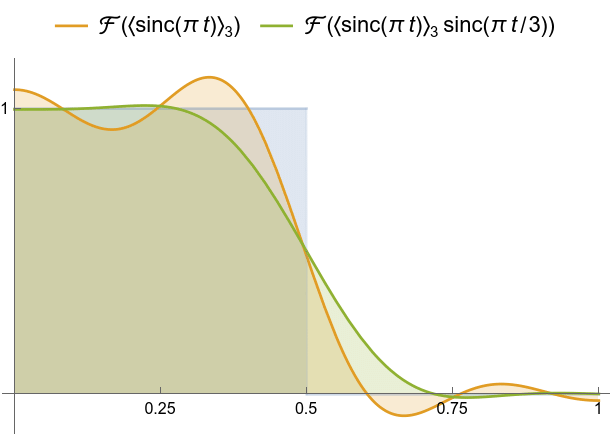
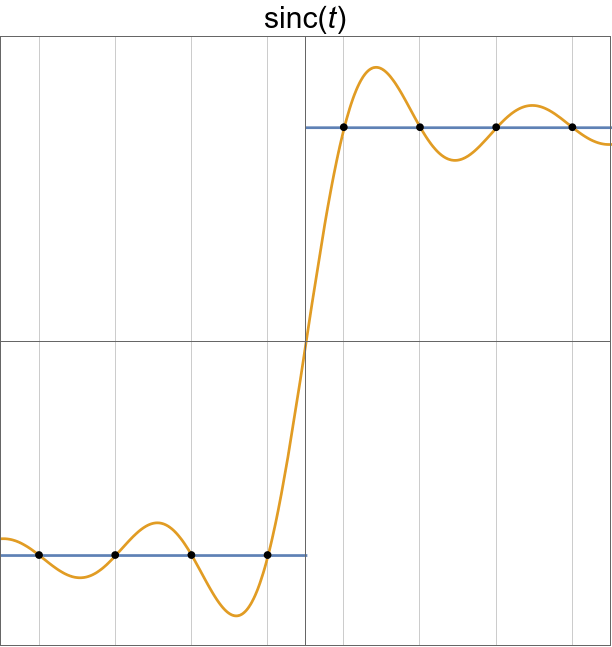
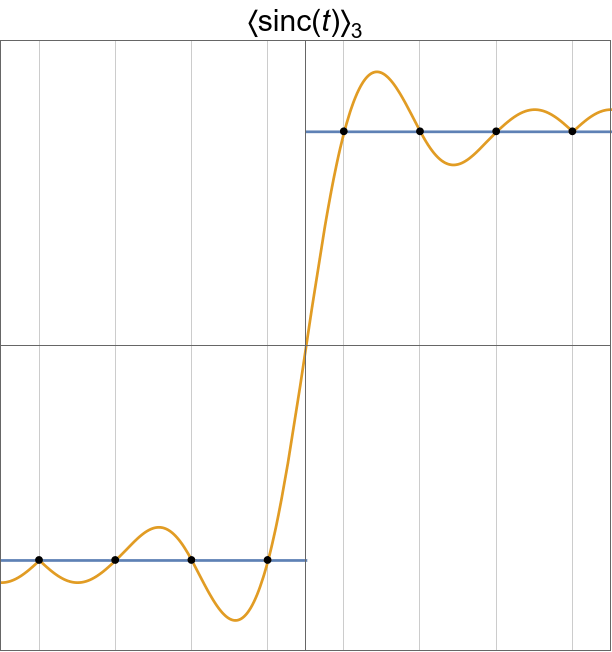
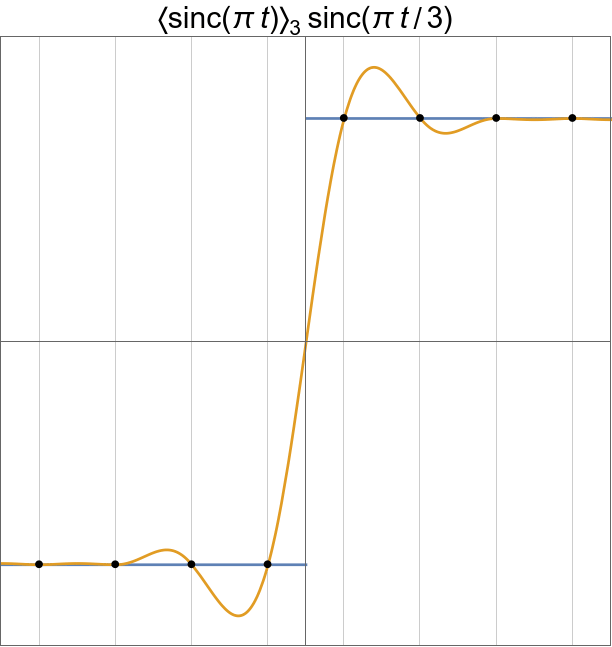