2021-05-01 Quick and dirty backpropagation in Haskell

In this post, we will train a simple neural network in Haskell using backpropagation. The network is a port of the example shown in micrograd. You can find code to run on GitHub.

While micrograd is about implementing automatic differentation, this post uses the ad library to do all the heavy lifting, instead focusing on building and training the network.

We will train a network to tell two semicircle shapes apart given labeled points belonging to the two shapes. We’ll call these shapes “moons”.

This animation shows how the network gradually learns where it thinks one moon ends and the other begins:

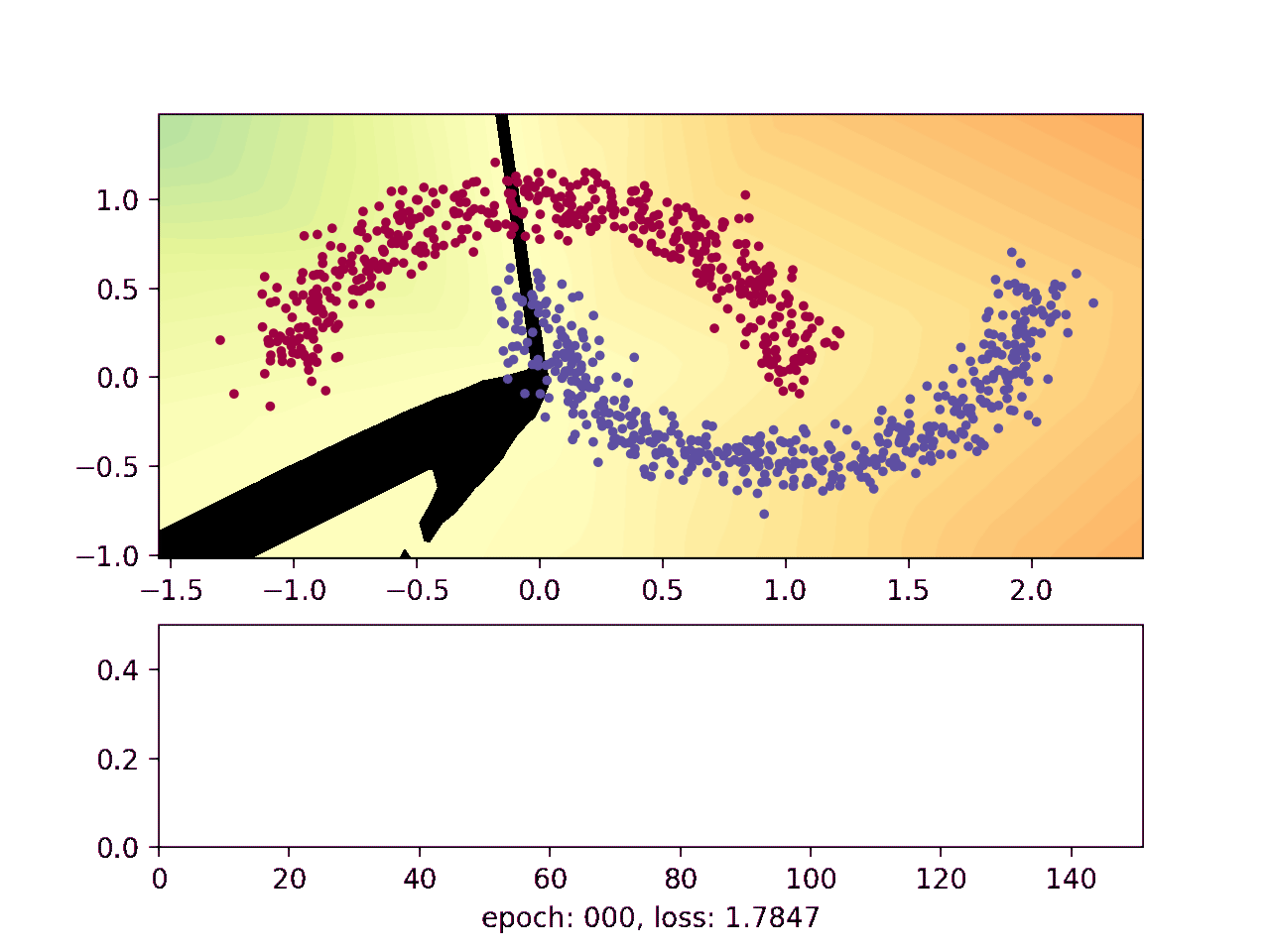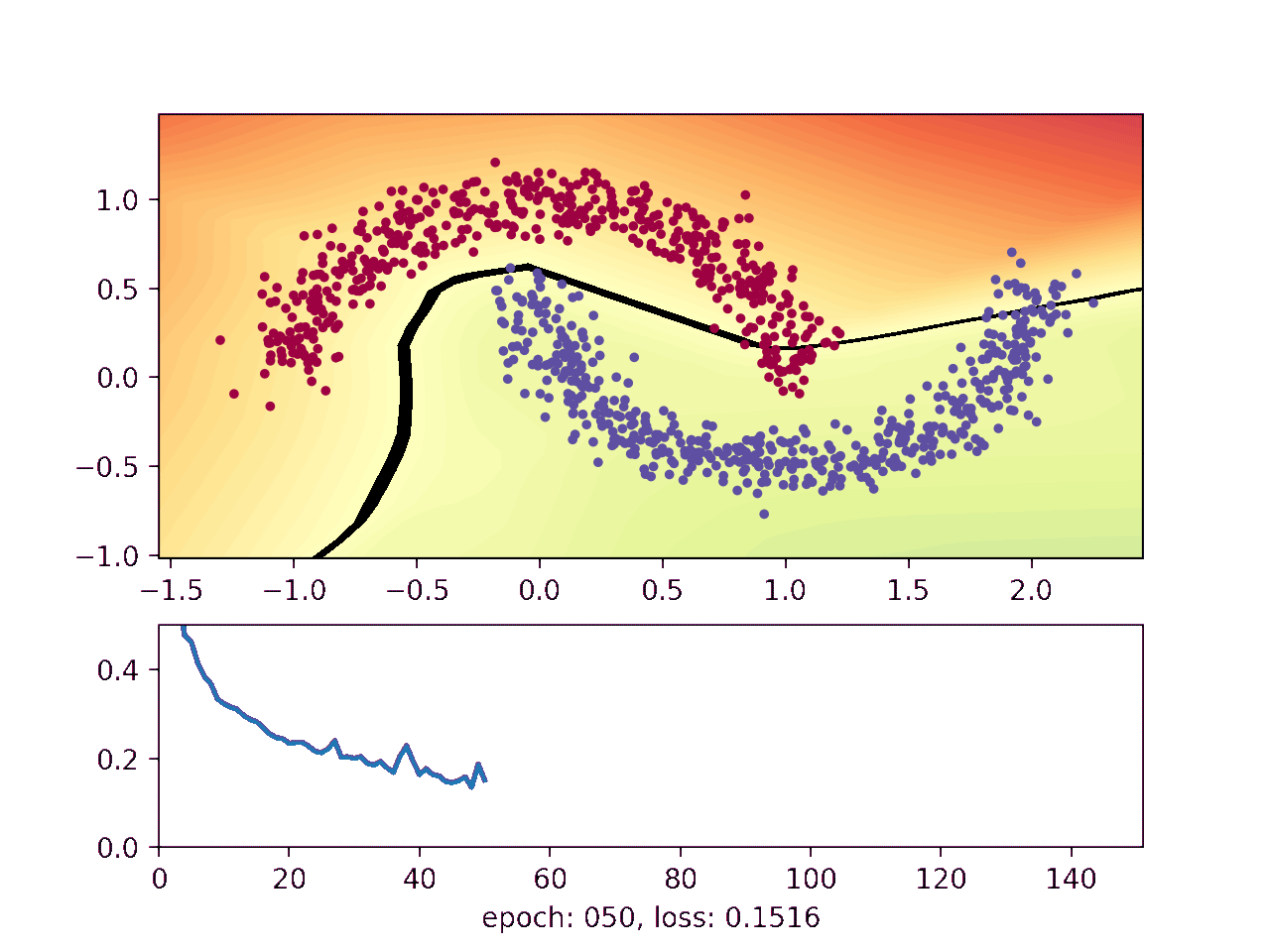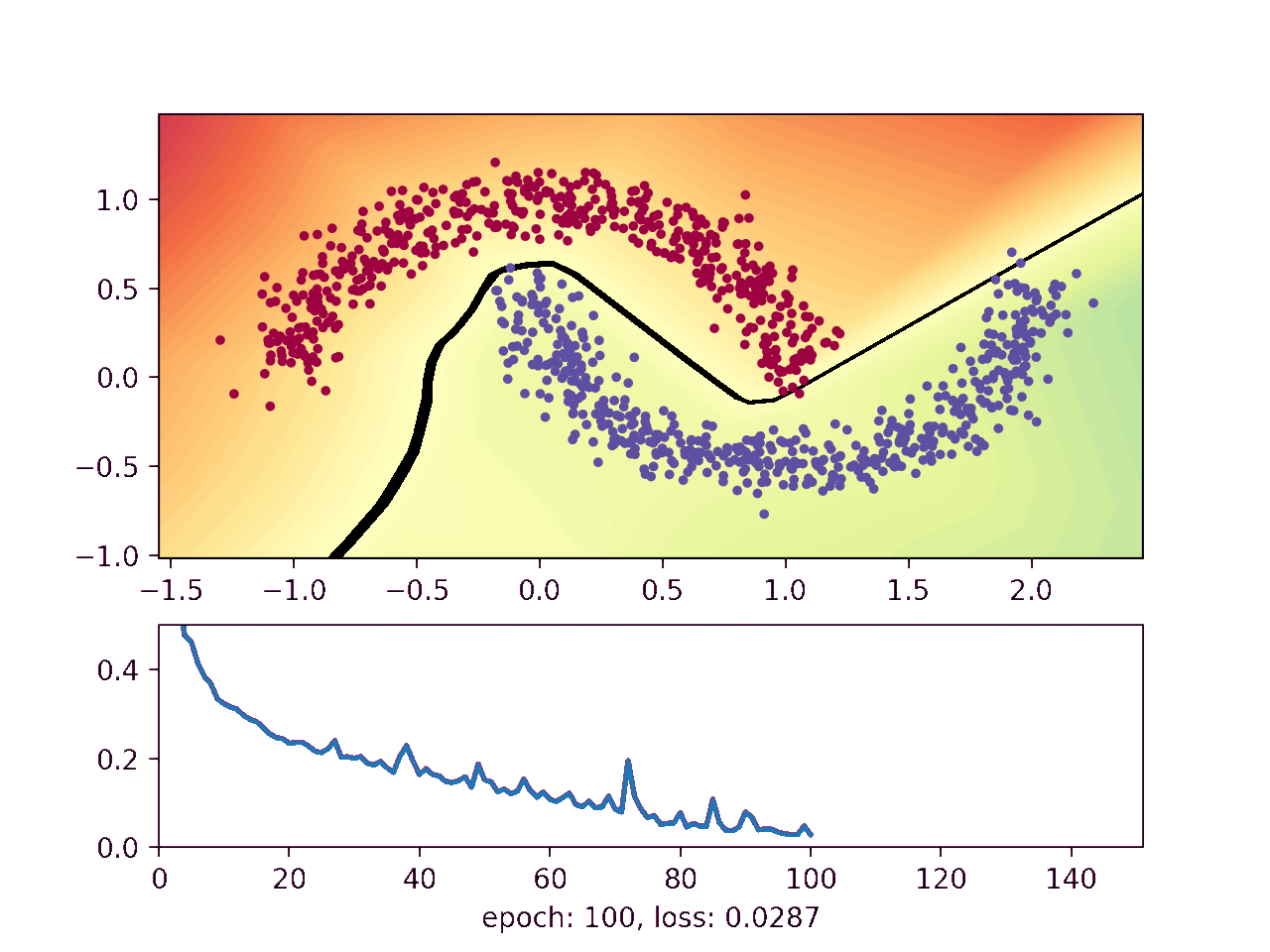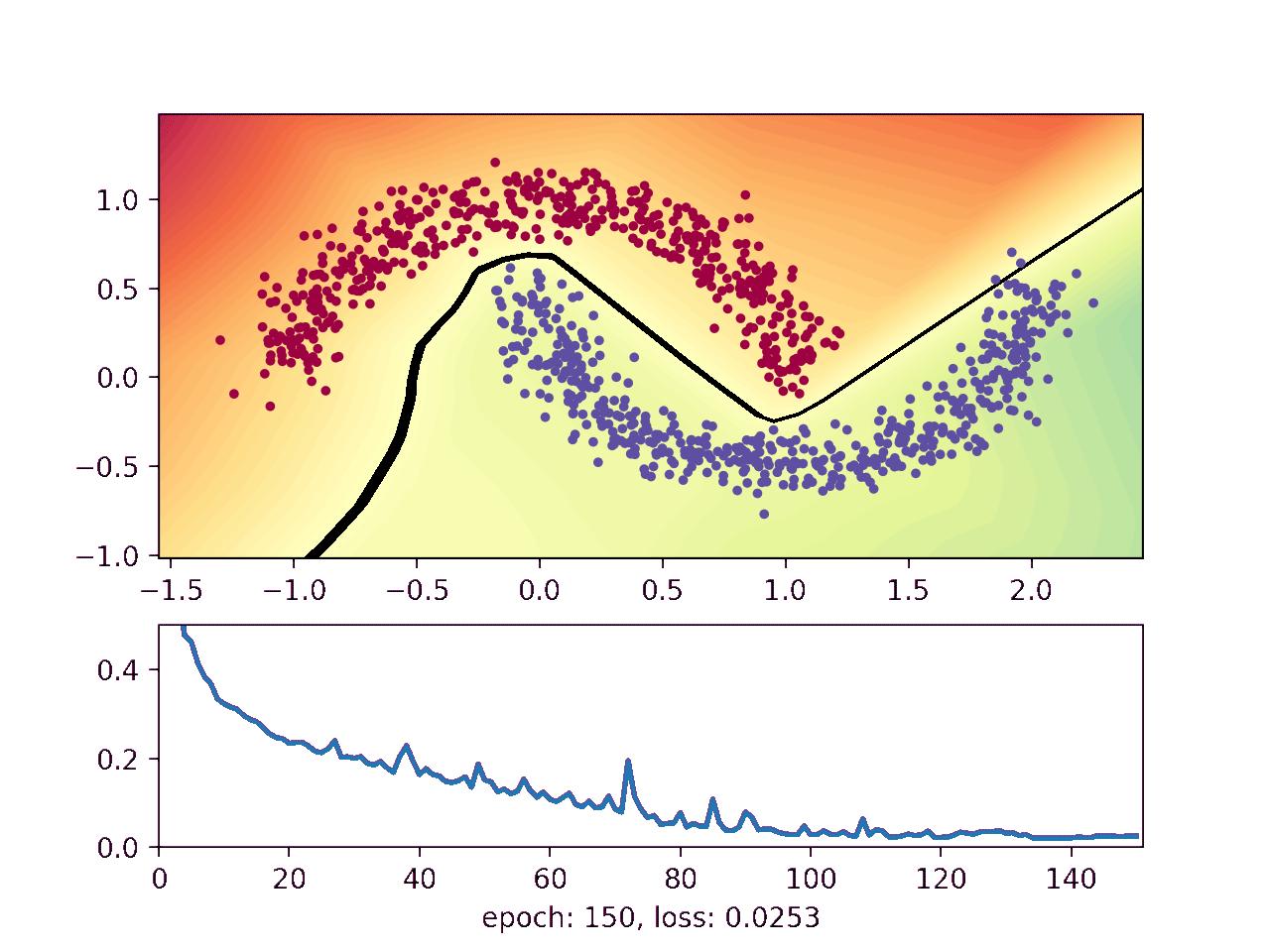
The blue and red points show a noisy sample from the two moons. The background on which the points are plotted on shows how the neural network thinks the moons should be classified, with the black line telling them apart. Finally, the lower plot shows how well the network is doing as the training advances.

The goal of this post is not to give a detailed primer on how deep learning works, but rather to shed some light on how backpropagation in particular lets us train neural networks. This means that we will gloss over many concepts and parameters to get to the heart of backpropagation quickly.

Multi-layer perceptrons in Haskell #

We’ll be using multi-layer perceptrons (from now on “MLP”) to implement our classifier.

A MLP looks like this:

Each MLP processes x_1, \dots, x_n inputs into y_1, \dots, y_m outputs. The inputs and outputs are all numbers. Our MLP will represent functions with signature \mathbb{R}^n \rightarrow \mathbb{R}^m.

Each neuron processes its inputs x_1, \dots, x_n as follows:

\phi(b + x_1 w_1 + \dots + x_n w_n)

where w_1, \dots, w_n are called the weights, b is the bias, and \phi is the activation function.¹ In Haskell:

import Data.Vector (Vector)
import qualified Data.Vector as V

data Neuron a = Neuron
  { weights :: Vector a
  , bias :: a
  } deriving (Eq, Show, Functor, Foldable, Traversable)

callNeuron :: (Num a) => Vector a -> (a -> a) -> Neuron a -> a
callNeuron xs activate neuron =
  activate (bias neuron + V.sum (V.zipWith (*) (weights neuron) xs))

We can assemble many neurons into a layer:

newtype Layer a = Layer (Vector (Neuron a))
  deriving (Eq, Show, Functor, Foldable, Traversable)

callLayer :: (Num a) => Vector a -> (a -> a) -> Layer a -> Vector a
callLayer inputs activation (Layer neurons) = V.map (callNeuron inputs activation) neurons

The layer forwards all the inputs to each neuron, getting one output per neuron.

Finally, the full MLP is a series of layers:

newtype MLP a = MLP (Vector (Layer a))
  deriving (Eq, Show, Functor, Foldable, Traversable)

We restrict ourselves to reLU as our activation function, which we will use in between every layer, but not on the output. We will also restrict the output to be a scalar. Putting it all together:

reLU :: (Num a, Ord a) => a -> a
reLU x = if x > 0 then x else 0

callMLP :: (Num a, Ord a) => MLP a -> Vector a -> a
callMLP (MLP layers) inputs =
  V.head $ callLayer
    (foldl' (\xs -> callLayer xs reLU) inputs (V.init layers))
    id
    (V.last layers)

So to recap:

• A neuron takes in n inputs and spits out a single output. Its signature is \mathbb{R}^n \rightarrow \mathbb{R}.
• We combine m neurons into a layer that has signature \mathbb{R}^n \rightarrow \mathbb{R}^m.
• We combine a bunch of layers into a MLP, with signature \mathbb{R}^n \rightarrow \mathbb{R}, where n is the number of inputs in the first layer.

We also derived Functor, Foldable, and Traversable instances for our MLP type. These type classes will let us inspect all the numbers contained in the MLP, which are none other than the weights and biases of each neuron of the MLP. We’ll put this capability to good use to train the network later on.

Telling moons apart #

We’re going to use a MLP to build a binary classifier. The data looks like this:

We want to train a network that learns to recognize the upper moon from the lower moon.

The inputs are the coordinates of the datapoint we want to classify, and the output will be a number telling us which moon it thinks the point belongs to.

The classifier should output -1 for inputs that belong to the upper moon, and 1 for inputs in the lower moon.

So the overall signature for our network will be \mathbb{R}^2 \rightarrow \mathbb{R}.

This is a good test bench for a neural network because simpler classifiers would not work so well, given how the two semicircles “interlock”, making them difficult to divide using a line or convex shapes.

Following micrograd, we use a network with two layers of 16 neurons each to solve this problem.

As expected, we initialize the network using random weights and no bias:

import qualified System.Random.MWC as MWC
import qualified System.Random.MWC.Distributions as MWC

initNeuron :: (MWC.Variate a, Num a) => MWC.GenIO -> Int -> IO (Neuron a)
initNeuron g inputs = do
  weights <- replicateM inputs (MWC.uniformR (-1, 1) g)
  return (Neuron (V.fromList weights) 0)

initLayer :: (Num a, MWC.Variate a) => MWC.GenIO -> Int -> Int -> IO (Layer a)
initLayer g inputs outputs = Layer <$> V.replicateM outputs (initNeuron g inputs)

-- | Initializes the MLP given the number of inputs of each layer.
-- The output is always a scalar.
initMLP :: (Num a, MWC.Variate a) => MWC.GenIO -> [Int] -> IO (MLP a)
initMLP g inputs =
  MLP . V.fromList <$> for (zip inputs (tail inputs ++ [1])) (uncurry (initLayer g))

-- Takes two coordinates as input.
initMoonClassifier :: (Num a, MWC.Variate a) => MWC.GenIO -> IO (MLP a)
initMoonClassifier g = initMLP gen [2, 16, 16]

However, we haven’t explained how to train the network yet! To do that, we’ll first take a small detour to explain automatic differentiation and gradient descent.

Automatic differentiation with ad #

Let’s say we have a function f : \mathbb{R}^n \rightarrow \mathbb{R} – that is, a function going from n numbers to a single number. Or in Haskell:

f :: [Double] -> Double

Reverse mode automatic differentiation (“reverse mode AD” or “AD” from now on) is an algorithm which lets us compute the partial derivatives of f with respect to each of the inputs.²

So, if we have a y = f(x_1, \dots, x_n), reverse mode AD will let us compute

\dfrac{\partial f}{\partial x_1} \cdots \dfrac{\partial f}{\partial x_n}

given any set of inputs x_1 \dots x_n. Throughout this blog post, we’ll call \frac{\partial f}{\partial x} at some specific input the “gradient” of x. Note that AD always computes specific gradients, rather than deriving a separate formula for the derivative of the function we’re studying.³

Back to Haskell: given our function f :: [Double] -> Double, we would expect automatic differentiation to look something like this:

-- | Given a function with many inputs and one output, and a specific
-- set of inputs, gives back the gradient for each input.
ad :: ([Double] -> Double) -> [Double] -> [Double]

This is essentially what the grad function from ad gives us:

-- The grad function calculates the gradient of a non-scalar-to-scalar
-- function with reverse-mode AD in a single pass.
grad ::
     (Traversable f, Num a)
  => (forall s. Reifies s Tape => f (Reverse s a) -> Reverse s a) -> f a -> f a

Let’s explain each of the differences:

• Traversable is used rather than lists, which allows us to compute gradients of any function which accepts “many” inputs – including lists or more complex data structures.
• Num a is used rather than Double, allowing to work with a wider range of base numeric types.
• The input function works on a mysterious Reverse s a, rather than on a. This type will store additional information on top of the base numeric types, which allows the gradients to be computed. In practice, this means that we will need to write all the functions we want to differentiate with a polymorphic number type, something that Haskell makes easy.

Now that we understand what grad can do for us, we can put it to the test:

% stack repl --package ad
> import Numeric.AD.Mode.Reverse
> grad (\[x,y] -> x * y + sin x) [1,2]
[2.5403023058681398, 1.0]
> grad (\[x,y,z] -> x * y * z) [1, 2, 3]
[6,3,2]

If you haven’t encountered AD before, I reccomend you verify these results by computing the derivatives of each function by hand and plugging the inputs in, and then stand back in awe of this truly neat algorithm.

Using ad for gradient descent #

ad also contains a useful helper function, gradWith, which lets us update the arguments of the function with their gradients:

gradWith ::
     (Traversable f, Num a)
  => (a -> a -> b) -- ^ Function to update the arguments
  -> (forall s. Reifies s Tape => f (Reverse s a) -> Reverse s a) -- ^ Function we're optimizing
  -> f a -- ^ Inputs to the function
  -> f b

We can use it to perform gradient descent or ascent on arbitrary functions.

Let’s consider the function

f(x, y) = 0.5 \times \mathrm{cos}(\frac{x}{2}) + \mathrm{sin}(\frac{y}{4})

and focus on the point (-3\pi, \pi):

We can use gradWith to iteratively make progress towards a peak:

> let f [x, y] = 0.5 * cos (x / 2) + sin (y / 4)
> let gamma = 4
> let points pt = pt : points (gradWith (\x dx -> x + gamma * dx) f pt)
> mapM_ (putStrLn . show) (take 5 (points [-3*pi, pi]))
[-9.42477796076938,3.141592653589793]
[-10.42477796076938,3.8486994347763406]
[-11.302360522659752,4.420436439971677]
[-11.89312422747638,4.869473384679192]
[-12.22342592418437,5.2155893225844725]

Note how we are making progress towards a peak, although progress slows down as the gradients get less steep.

gamma is the so-called step size or learning rate, which determines how much we “move” the point along the gradient at each step. Here we’ve picked 4 since it looked good on the graph.

Also note that here we’re adding to the input (x + gamma * dx) since we want to maximize the function. If we were to perform gradient descent we would subtract instead.

Training a MLP with backpropagation #

Backpropagation is the application of gradient descent powered by automatic differentiation to train neural networks.

Let’s repeat how gradient descent with automatic differentiation works:

• We have a function f : \mathbb{R}^n \rightarrow \mathbb{R}.
• We want to find an input to f which minimizes its output.
• We pick a starting point x_1, \dots, x_n.
• We iteratively update our current point to be x_1 - \gamma \frac{\partial f}{\partial x_1}, \dots, x_n - \gamma \frac{\partial f}{\partial x_n}, getting the gradients at each step with automatic differentiation.
• We terminate the procedure when the output stops improving or some other termination condition is satisfied.

So the “output” of gradient descent is the set of inputs which minimized f.

Backpropagation works by defining a loss function which measures how well the network is doing, and then performing gradient descent on all the weights and biases contained in the network to minimize the loss.

Let’s go back to our MLP classifier. It contains:

• A first layer made out of 16 neurons with 2 inputs, for a total of 16 \times 2 weights and 16 biases;
• A second layer made out of 16 neurons with 16 inputs (the outputs to the previous layer), for a total of 16 \times 16 weights and 16 biases;
• A third layer made out of 1 neuron with 16 inputs, for a total of 16 weights and 1 bias.

So we’ll want to perform gradient descent on a function \mathrm{loss} : \mathbb{R}^{337} \rightarrow \mathbb{R}, updating the weights and biases to give us lower loss at each step. When people say that GPT-3 has 175 billions parameters, this is what they are referring to.

But what shall the loss function be? This is where the training data comes in. We pick input-output samples which we know are correct, and measure how much our current network strays from them. The bigger the difference, the bigger the loss.

For the purpose of this network we’ll use the following loss function, which works well for this case. However the details are unimportant to understand how backpropagation works.

-- See <https://github.com/karpathy/micrograd/blob/c911406e5ace8742e5841a7e0df113ecb5d54685/demo.ipynb>
loss :: (Fractional a, Ord a) => MLP a -> Vector (Vector a, a) -> a
loss mlp samples = let
  mlpOutputs = V.map (callMLP mlp . fst) samples
  -- svm "max margin" loss
  losses = V.zipWith
    (\(_, expectedOutput) mlpOutput -> reLU (1 + (- expectedOutput) * mlpOutput))
    samples
    mlpOutputs
  dataLoss = V.sum losses / fi (V.length losses)
  -- L2 regularization
  alpha = 1e-4
  regLoss = alpha * sum (fmap (\p -> p * p) mlp)
  in dataLoss + regLoss

• We first compute the output that the MLP gives us for each of the input in the training data.
• We compute the average hinge loss for our samples. This loss measure is useful for classifiers that should return -1 or 1. Intuitively, the loss will linearly increase as the MLP output disagrees with the expected output.
• We perform L2 regularization on the parameters of the MLP, using its Functor instance. Intuitively, this helps to keep the weights and biases small, which results in “simpler” and hopefully more general models.
• We add these two terms to get the overall loss.

We can then use gradWith to perform a gradient descent step given some training data:

import qualified Numeric.AD.Mode.Reverse as AD

optimizeStep ::
     (Floating a, Ord a)
  => MLP a -> Vector (Vector a, a) -> a -> MLP a
optimizeStep mlp samples learningRate =
  AD.gradWith
    (\x dx -> x - learningRate * dx)
    (\ad_mlp -> loss
        ad_mlp
        (V.map (\(inputs, output) -> (V.map AD.auto inputs, AD.auto output)) samples))
    mlp

The update rule for gradWith is exactly the same as the one in our previous example, although we’re descending and therefore subtracting.

The AD.auto is used to “lift” constants (in this case our samples) into the numeric type that is used by ad to compute the gradients.

This is in essence what backpropagation is about: we minimize the loss function by performing gradient descent on all the weights and biases in our network. The name derives from the fact that reverse-mode automatic differentiation computes the derivatives “backwards” from the output to the inputs.

We can do this iteratively, for a series of training data sets (also known as “batches”), to incrementally refine our weights and biases:

-- | Given an initial model, and batches to train the model on,
-- iteratively trains the model returning each intermediate one.
optimize ::
     (Floating a, Ord a)
  => MLP a -> [Vector (Vector a, a)] -> [MLP a]
optimize mlp batches =
  scanl
    (\mlp (epoch, batch) -> let
        learningRate = 1.0 - 0.9 * fi epoch / fi numEpochs
        in optimize mlp batch learningRate)
    mlp0
    (zip [0 :: Int ..] batches)
  where
    numEpochs = length batches

The learning rate decreases at each step, starting from 1 and ending at 0.1: we want to make rapid progress at the beginning and slow down as we settle on a solution at the end.

Note that each batch might be different from the others, which means that we’d be optimizing a different function each time, although each batch would be drawn by same data set.

Using 150 batches of 50 randomly generated points each, and testing it on a testing set of 1000 randomly generated data points, we can witness how the network gets better and better at classifying our moons:

The black line indicates where the neural network flips from negative to positive, which is where the network currently thinks the upper moon ends and the lower moon begins. It starts out random when the weights are initialized, and then gradually gets better at distinguishing the two moons.

You can find the full code here. Excluding generating and plotting the data, the whole task is completed in around 100 lines of code.

Closing remarks #

This example is meant to illustrate the basic building blocks of backpropagation – it is not a primer on how to actually implement it! While ad is fantastically easy to use, it is also fantastically slow for this sort of application.

That said, if you did follow the steps in this post, you now understand the key machinery that powers that deep learning thing everybody is going crazy about 🙃.