2024-06-30 CRCs and Reed-Solomon coding: better together

In my latest filesystem-themed post I discussed a technique to perform distributed resource management more safely. If you haven’t read that post you should do so – it is short and describes the key components involved in this post.

This time I’ll explain how one might effectively combine Reed-Solomon coding and cyclic redundancy checks.1 The first gives us redundancy (we can lose disks and still recover our data), the second protects us against data corruption.

Let’s start with a brief introduction to both these primitives.

The primitives #

CRCs #

You probably already know or have heard about cyclic redundancy checks. In this context you can think of them as fast non cryptographic hashes, which are useful for detecting data corruption.2

In this post we’ll be using the CRC-32C variant, 32 standing for “32 bits” (as in, the “hash” is 32-bit wide), and C standing for “Castagnoli”, the generator polynomial we’ll be using.3 The generator polynomial determines how big our checksums will be, alongside other properties. Predictably CRC-32C will produce 32-bit polynomials.

The type signature for our CRC-32C function looks something like this:

// Given the CRC so far, updates it to include `data`. Start
// with `crc = 0`.
uint32_t crc32c(uint32_t crc, size_t size, const char* data);

We pass some data in and we get a 32-bit wide CRC for said data. The function allows us to compute CRCs as the data is streaming in, rather than all at once. CRCs can then be stored and then used to check if the data has been corrupted somehow. For state of the art implementations of CRC-32C, head over to Peter Cawley’s fast-crc32 repo.

Reed-Solomon coding #

You can find a short post on the high level idea behind Reed-Solomon coding on this blog, and a more detailed implementation manual Peter’s blog.4 But in short, our flavor of Reed-Solomon gives us the following functions:

// Given `D` equally sized data chunks in `data`, each of
// `size` length, write out `P` parity chunks in `parity`.
void rs_compute_parity(
  size_t size,
  uint8_t parity,    // high nibble = D, low nibble = P
  const char** data, // input, shape [D][size]
  char* parity       // output, shape [P][size]
);

// Given at least `D` chunks (data or parity), recover
// up to `P` chunks (data or parity).
void rs_recover(
  size_t size,
  uint8_t parity,      // low nibble = D, high nibble = P.
  uint32_t present,    // D+P wide bitmask, popcount(present) >= D
  uint32_t to_recover, // D+P wide bitmask, popcount(to_recover) <= P
  char** data,         // input/output, shape [D][size]
  char* parity         // input/output, shape [P][size]
);

We’ll refer to Reed-Solomon coding with D data chunks and P parity chunks as \mathrm{RS}(D,P). We can pack D and P in a single 8-bit number since we don’t need D or P to be larger than 15.

Concretely, if we have a 50MiB file, we can use \mathrm{RS}(10, 4) to split it in 10 5MiB chunks, and then generate 4 5MiB parity chunks. We can then scatter these 14 chunks across 14 different drives. Under normal operations readers would just utilize the 10 data chunks. But if one or more data chunks are missing or corrupted readers would be able to recover them – assuming that the total number of missing chunks is not greater than four.

Using CRCs and RS together #

Recall that our filesystem is made out of metadata servers, storage nodes, and clients. We split the files into blobs so that we can have an upper bound on the blob size (say 100MiB). This is just a nice to have – it ensures that the unit of work is reasonable.

On the data structures held by the metadata servers, things would look like this:

struct chunk {
  uint64_t drive_id; // where the chunk is stored
  uint64_t chunk_id; // a unique identifier for the chunk
  uint32_t crc;      // CRC-32C of the chunk
};

struct blob {
  uint32_t size;         // size <= chunk_size*D
  uint32_t crc;          // CRC32-C of the whole blob
  uint32_t chunk_size;
  uint8_t parity;        // low nibble = D, high nibble = P
  struct chunk chunks[]; // length D+P
};

struct file {
  uint64_t file;
  uint32_t num_blobs;
  struct blob blobs[]; // length num_blobs
}

We won’t really be concerned with files from now on, since once you can read and write blobs reading and writing files is trivial, considering that our files are written once and never modified.

In practice it is convenient to store chunks with sizes that are multiples of 4KiB (x86’s page size), since it simplifies bookeeping in kernel modules and in the storage node software.5 If the blob size is not a multiple of D \times 2^{12} the data section will contain trailing zeros.

When a client needs to write a blob, it splits it in D chunks, and computes the CRC-32C for each.

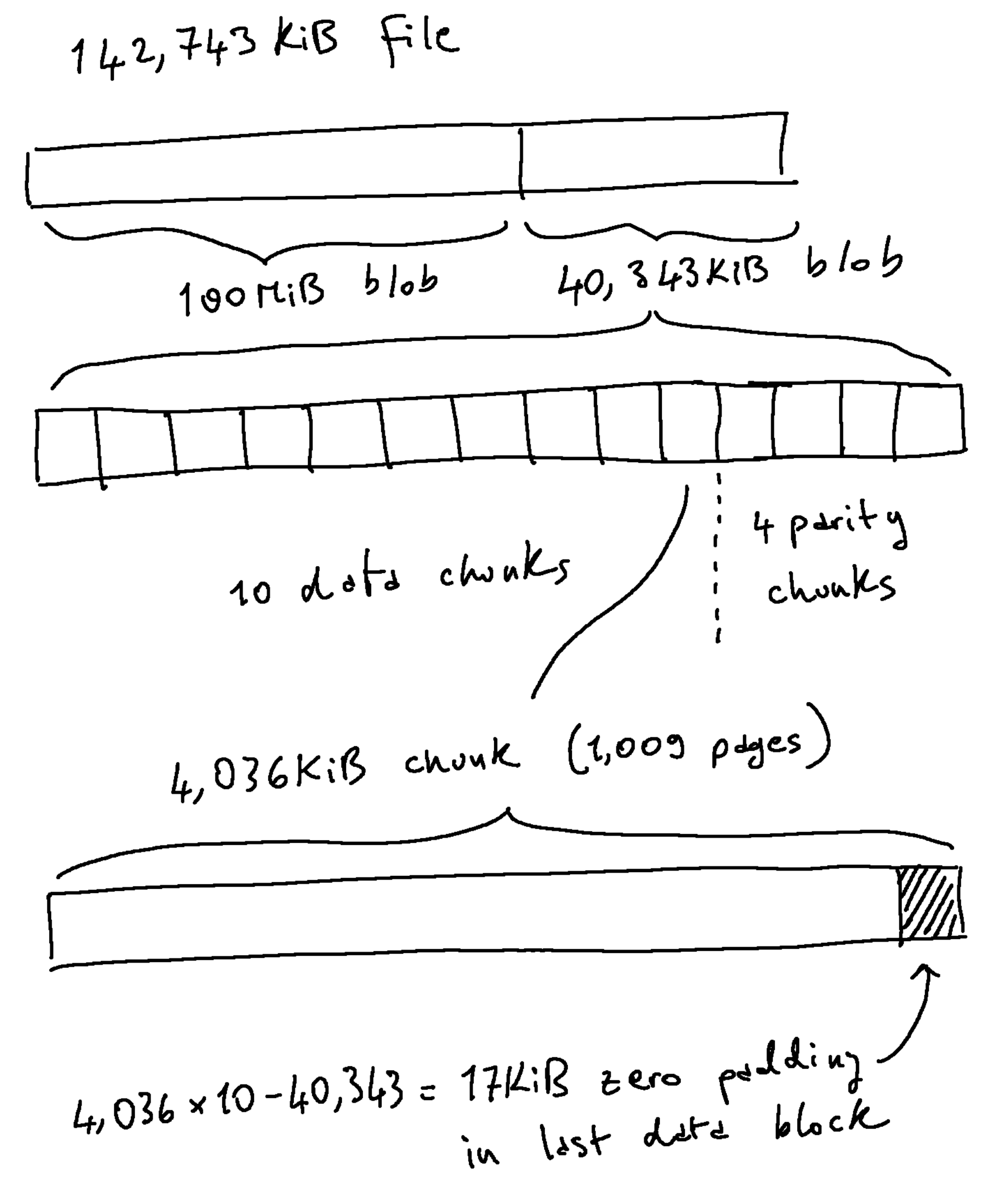
The diagram above shows how a 142,743KiB file might be split in two blobs. For the highlighted 40,343KiB blob, the first data chunk will span bytes [0, 4,036KiB), the second [4,036KiB, 8,072KiB), and so on. Since we want the chunks to be 4KiB aligned the last data block will contain 17KiB of unused space, which we zero out.

When a client wants to read the blob at a certain offset, it just has to reach within the correct data chunk. If for whatever reason the data chunk cannot be read, it can be recovered by reaching into the other data chunks and the parity chunks. Note that rs_recover works just fine with reads internal to the chunks, i.e. we do not need to read the entire chunks to recover parts of them.

Arbitrary offset reads #

Reading at random offsets within a chunk presents a challenge. We want to CRC-validate every byte we fetch from the filesystem, to ensure that no corrupt reads ever happen. We also want to delegate all CRC and RS computation to the clients, to distribute this CPU overhead to the clients.6

However the CRCs we store in the metadata are concerning an entire chunk. Consider again the case of our 40,343KiB blob using \mathrm{RS}(10,4). Each data chunk will be ~4MiB. If we want to read 256KiB starting from offset 31MiB, while checking what we read against our CRC, we’d have to read the 7th chunk in its entirety, incurring in 16x read amplification.

To avoid incurring in this amplification, we can store a CRC for each page directly in the storage nodes. The client will check the CRCs as it processes pages, repairing corruption if it encounters it by using the other chunks.

Note that storing the block CRCs in the metadata is still a good idea: it’s very cheap and lets us implement the checking scheme described in the previous post, together with other safety checks we’ll describe next. On the other hand, storing the CRCs for all the pages in the metadata servers would increase the metadata size by two orders of magnitude.

Checking CRCs on the metadata servers #

As hinted in the previous post, we trust the clients to not be malicious, but not to be correct. The scheme described so far has no safeguards to make sure that the file is chunked correctly by the clients. Luckily some safeguards can be added at no costs.

Thanks to the properties of CRCs, the following functions can be implemented:7

// Given CRCs for `a` and `b`, computes the CRC of the pointwise XOR
// of `a` and `b`.
//
//   crc32c_xor(size, crc32c(0, size, a), crc32c(0, size, b)) =
//   crc32c(0, size, [x^y for (x, y) in zip(a, b)])
uint32_t crc32c_xor(size_t size, uint32_t crc_a, uint32_t crc_b);

// Given CRCs for `a` and `b`, compute the the CRC of `a` concatenated
// with `b`. Only the size for `b` is needed, and the sizes may differ.
//
//   crc32c_append(crc32c(0, size_a, a), size_b, crc32c(0, size_b, b)) =
//   crc32c(crc32c(0, size_a, a), size_b, b)
uint32_t crc32c_append(uint32_t crc_a, size_t size_b uint32_t crc_b);

// Given CRC for `a`, gives the CRC we'd get by adding `n` zero
// bytes at the end of `a`.
//
//   crc32c_add_zeros(size_a, crc32c(0, size_a, a), n) =
//   crc32c(crc32c(0, size_a, a), n, [0]*n)
uint32_t crc32c_add_zeros(uint32_t crc, size_t n);

// Given CRC for `a + [0]*n`, that is the CRC for a
// bytestring with `n` trailing zeros, gives the CRC
// of `a` without the trailing zeros.
//
//   crc32c_remove_zeros(crc32c(0, size_a+n, a + [0]*n), n) =
//   crc32c(0, size_a, a)
uint32_t crc32c_remove_zeros(uint32_t crc, size_t n);

These functions allow us to perform some useful sanity checks on the chunked data, without looking at the data – following the same theme as the previous post.

crc32c_append and crc32c_remove_zeros will be used to check that concatenating the data chunks will give us the CRC of the whole blob. crc32c_remove_zeros is needed since as we’ve seen the data chunks might contain trailing zeros which we must remove from the CRC.

crc32c_append_zeros also opens up the possiblity of having the blob to be larger than the sum of the data chunks, in case it contains trailing zeros. This allows us to encode large holes in files without taking any storage space.

Moreover, we can setup the first parity chunk to be the XOR of the data chunks.8 This allows us to also check that the data chunks’ CRCs agree with the first parity chunk’s CRC through crc32c_xor. Sadly, it is not possible to generate the CRCs of the rest of the parity chunks without looking at the contents.

Again, these measures are not really concerned with adversarial cases, but they do catch a very large set of client bugs.

Wrapping up #

The scheme described in this post is just about how to lay the data to exploit CRCs and RS effectively. It’s not a complete recipe to ensure the integrity of the filesystem! Many other measures were implemented in our filesystem to reduce the chance of losing data, including:

I plan to explore the topics above in future blog posts.

Acknowledgements #

Thanks to Alexandru Scvorţov, Shachaf Ben-Kiki, and Peter Cawley for reading drafts of this blog post.

f@mazzo.li · twitter · mastodon · source