2022-10-07 Lánczos interpolation explained

1. A lot of the maths is also worked out in a Mathematica notebook.↩︎

2. Cubic interpolation is not included in the showcase since it is a family of filters rather than a single filter — most cubic filters used in practice end up looking similar to Lánczos, although probably a bit less sharp but with less ringing.↩︎

3. The images use a 3-lobed Lánczos interpolation.↩︎

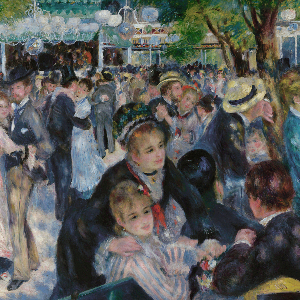We will proceed as follows:

1. A description of the problem we’re trying to solve;
2. How interpolation can be phrased in terms of convolutions;
3. An introduction to \mathrm{sinc}, the “best” interpolation function, together with a quick recap on Fourier transforms;
4. A concrete example of interpolating with \mathrm{sinc};
5. Why we can’t and shouldn’t use \mathrm{sinc} directly;
6. How \mathrm{sinc} can be modified to make it work well in practice;
7. Some closing thoughts.

If you’re already familiar with Fourier analysis, section 6 might still be of interest, given that it explains the main ideas behind Lánczos interpolation.

Let’s get started.

The problem #

When resizing an image, we generally have a specific target size in mind. In this post, we focus on the general problem of “filling in” the gaps between regularly spaced samples — that is, interpolating. Once we know how to interpolate between samples, we can resample at will, including downsampling and upsampling.

Let’s consider the 1-dimensional case — we’ll see shortly how to extend 1D interpolation techniques to two dimensions. Here’s a 1-dimensional signal sampled at a fixed interval:

We’ll generally call the “original” signal from which the samples are taken f(t), and refer to the input as “time” to go along with digital signal processing terminology.

Linear interpolation is just connecting the dots:

We’ll call the interpolated signal \bar{f}(t), shown above in gold. More samples mean better interpolation:

4. In practice, when imaging software performs “cubic interpolation”, it is not actually fitting polynomials to points.

   Instead, it usually performs something quite similar to Lánczos interpolation, with the goal of having the output resemble what we’d get if we actually fit polynomials.

   ImageMagick has a long list of such cubic filters — see Catmull-Rom or Mitchell filters for examples of cubic filters which resemble Lánczos.↩︎

Interpolation and convolution #

It is mathematically and practically helpful to frame interpolations as convolutions.

Let’s imagine that our signal f(t) is sampled at regular intervals so that they are 1/\xi apart from each other. We’ll say that \xi is the frequency at which the samples are taken – the higher the frequency, the denser the samples. We’ll also use \xi to talk about frequencies in the spectrum of f(t) later on, and relate the two.

For instance, using our previous function and \xi = 2:

We’ll refer to a single sample with f_k, where f_k is taken at time k/\xi. Given some interpolation function g, we can convolve it with our discrete samples to get an interpolated signal \bar{f}(t):

\bar{f}(t) = \sum_{k = -\infty}^{+\infty} g(t - k/\xi) \, f_k

If the sum above is a bit opaque, don’t worry, visual aid is coming shortly.

Within this framework, linear interpolation can be seen as interpolating with an appropriately scaled triangle function:

The first thing to note is that when g(t) = \mathrm{triangle}(\xi t), convolving at the sample points will not change them. Or in other words, the convolution at k/\xi will multiply f_k by 1, and all the other f_ks by 0, with the result of having \bar{f}(k/\xi) = f(k/\xi):

Let’s see this in action when \xi = 2, and t = -3/\xi:

We’re showing the interpolating function \mathrm{triangle}(t) in green, the green points are each term of the convolution sum, and the gold point is the interpolated point (that is, the sum of the green points, which is the convolution).

As you can see, the only point that contributes is f_{-3} = f(-3/2). Note that the only non-zero green point is hidden behind the gold point – since they have the same value.

Leaving the samples intact is a desirable and guiding property for interpolating functions.

Between sample points is where things get interesting:

The triangle will mix the two points to its left and right, producing the linear interpolation in the middle. Running the convolution at every point, we get back our linear interpolation:

The triangle function is a very basic option, but we’ll soon discuss a fancier interpolation function.

\mathrm{sinc}, master interpolator #

We now get talking about \mathrm{sinc}, which is the basis for Lánczos interpolation and many other interpolation filters.

\mathrm{sinc} is defined as

\mathrm{sinc}(t) = \frac{\sin t}{t}

The hole at t = 0 is plugged by setting \mathrm{sinc}(0) = 1. It looks like this:

The first good property of \mathrm{sinc} is that it interpolates well in the sense that it keeps samples intact: we have \mathrm{sinc}(0) = 1, and then we have evenly spaced zeros. By default the zeros are spaced by \pi, but we can scale it to work with any frequency \xi using \mathrm{sinc}(\pi \xi t):

Just like with \mathrm{triangle}, the samples are preserved, given the very conveniently placed zeros. But just like before, the interesting case is when we’re interpolating between samples:

I’ve centered the interpolation point to better show what happens to the sides. While \mathrm{triangle} considers only the two closest points, \mathrm{sinc} considers an infinite number of points to its left and right.

This is what the full interpolation looks like for our function:

Nice and smooth!

Beyond being a well-behaved interpolating function, \mathrm{sinc} has a second property which makes it special in this realm.

Before going forward, let’s recap on a few Fourier ingredients:

• A very large class of functions can be represented as the sum of \cos \pi \xi and \sin \pi \xi oscillations (or frequencies).

• The Fourier transform \mathcal{F}\{f(t)\}(\xi) of f(t) tells us “how much” of a frequency \xi is present in f(t).

• \mathcal{F}\{f(t)\} uniquely determines f, and vice-versa.

5. We’ll use Fourier transform and spectrum and frequency response interchangeably.↩︎

6. We’re doing two common things to simplify the Fourier transform plots:

   • We plot the positive part only since the functions we’re analyzing are real-valued, and therefore the negative side will be identical.
   • We plot the absolute value of Fourier transform, which is complex-valued. This is usually what we want, but in this case it is also irrelevant since the interpolation functions we’re analyzing are all even, and therefore only contain \cos frequencies.

   We’re using Mathematica to both compute and plot the frequency response – see the function FT in the notebook.↩︎

With \xi = 2 the spectrum is now of width 1, although with halved magnitude. The halving is compensated by the fact that we have double the zeros (that is, double the samples when interpolating).

When we’re interpolating by convolving we’re adding up scaled versions of \mathrm{sinc}:

\bar{f}(t) = \sum_{k = -\infty}^{+\infty} \mathrm{sinc}(\xi \pi (t - k/\xi)) \, f_k

7. I’m being pretty handwavy here, but you can convince yourself of this mathematically too since the Fourier transform is a linear operator, and given that translation does not change the width of the spectrum.↩︎

8. The original landmark paper is still one of the clearest sources for an explanation of the theorem and its mathematical details.↩︎

\mathrm{sinc} in practice #

Let’s put this knowledge in action with our example function, which just so happens to be formed of three individual frequencies:

f(t) = \sin \pi \frac{t}{5} + \frac{1}{2}\cos \pi t + \frac{1}{3}\sin \pi 2 t

Usually, the Fourier transform of a function will be continuous. However, since we’re dealing with three isolated frequencies, for this signal it will not even be a proper function, but rather one impulse for each of the three frequencies. We might plot as follows:

Shannon-Nyquist tells us that that we need to sample at a frequency greater than twice the maximum frequency in the spectrum. In this case the maximum frequency is 1, so we need to sample using some \xi > 2. If we do that and convolve with a scaled \mathrm{sinc}, we should reconstruct the signal exactly:

9. This is why this post and most sources are careful to state we need to sample at a rate greater than \xi.↩︎

The problem with \mathrm{sinc} #

Now that we know about how convolving with \mathrm{sinc} interpolates points, we still face problems. The first problem is evident: to convolve with \mathrm{sinc}, we need to consider all the samples we have every time. This is clearly impractical: we’d need to look at every pixel in the input image to generate each pixel in the output!

The second problem is what happens when our spectrum is not of limited width. Let’s consider a simple stepping function, and its spectrum:

As you can see, the spectrum of \mathrm{sgn}(t) tapers but never reaches zero. This makes sense: to identify the precise moment where the function goes from -1 to +1, we’d need samples with no distance between them. So we can never reconstruct this function exactly with a finite number of samples.

That said, one might still be surprised at how poorly \mathrm{sinc} performs in situations like this:

10. In this case, the reconstructed signals are very close to (although not exactly the same as) the “sine integral” function:

    \mathrm{Si}(z) = \int_0^z \mathrm{sinc}(t) \, dt ↩︎

\mathrm{sinc}, chopped and screwed #

Let’s first consider the problem of \mathrm{sinc} extending into infinity, and therefore requiring to examine all samples. Our first attempt to solve this issue might be just to just set \mathrm{sinc} to zero outside a certain window:

This allows our convolution to be made up of “only” 7 terms, rather than an infinite number of terms. For images, that would be 7 \times 7 = 49 terms, given we need to go in both dimensions. Not a tiny number, but manageable.

We’ll refer to function set to zero when |t| \ge a as \langle f(t) \rangle_a:

\langle f(t) \rangle_a = \begin{cases} f(t) & \text{if}\ -a < t < a, \\ 0 & \text{otherwise}. \end{cases}

How will \langle \mathrm{sinc} \rangle_3 fare as an interpolation function? The first thing to notice is that we’re still stuck with the Gibbs oscillations in the reconstructed signal:

In images, this shows up in so-called “ringing” artifacts:

Those “echoes” around the letters are the same phenomenon as the wobbles in our reconstructed step function. They are particularly evident in images when text is present – the glyphs’ edges being our jump discontinuities.

However, to characterize how \langle \mathrm{sinc} \rangle_a fares mathematically we can again look at its spectrum compared to \mathrm{sinc}’s. Here’s the spectrum of \langle \mathrm{sinc} \rangle_a with a set to 3, 5, and 10 respectively:

11. Lánczos actually developed these techniques to deal with truncated Fourier series rather than truncated interpolation functions, but exactly the same line of reasoning applies.↩︎

\begin{equation*} \begin{split} \mathcal{F}\{f(t)\}(\xi) = & \int_{-\infty}^{+\infty} f(t) \, e^{-2 \pi i \xi t} \, dt \\ f(t) = &\int_{-\infty}^{+\infty} \mathcal{F}\{f(t)\}(\xi) \, e^{+2 \pi i \xi t} \, d\xi \end{split} \end{equation*}

As usual we’re packing both \sin and \cos oscillations together using Euler’s formula:

e^{i x} = \cos x + i \sin x

The Fourier transform picks out how much a given frequency contributes to the function by looking how much they “line up”.

What we want to do is modify \langle f(t) \rangle_a so that its spectrum is as close as possible to that of f(t). Our starting point will be characterizing the nature of the error in the spectrum more precisely. First, let’s split the spectrum of f(t) in three parts:

\mathcal{F}\{f(t)\}(\xi) = \int_{-\infty}^{-a} f(t) e^{-2 \pi i \xi t} \, dt + \int_{-a}^{+a} f(t) e^{-2 \pi i \xi t} \, dt + \int_{+a}^{+\infty} f(t) e^{-2 \pi i \xi t} \, dt

The error for the spectrum of \langle f(t) \rangle_a will be the first and third term:

\mathcal{F}\{f(t)\}(\xi) - \mathcal{F}\{\langle f(t) \rangle_a\}(\xi) = \int_{-\infty}^{-a} f(t) \, e^{-2 \pi i \xi t} \, dt + \int_{+a}^{+\infty} f(t) \, e^{-2 \pi i \xi t} \, dt

These are the annoying oscillations we see for our truncated \mathrm{sinc}s, and that we do not want. Considering only the right hand side of the sum above, and reworking it a bit, we get:

\begin{equation*} \begin{split} \int_{+a}^{+\infty} f(t) \, e^{-2 \pi i \xi t} \, dt & = \int_{0}^{+\infty} f(t+a) \, e^{-2 \pi i \xi (t + a)} \, dt\\ & = e^{-2 \pi i \xi a} \int_{0}^{+\infty} f(t+a) \, e^{-2 \pi i \xi t} \, dt \end{split} \end{equation*}

12. As remarked in a previous footnote, here we can get away with only considering \cos, since the functions we’re analyzing are even.

    Also, the absolute, 20x downscaled \cos 2 \pi \xi 3 is plotted, so that it can be better shown together with the error.↩︎

Lánczos’ next step was to “smooth out” the undesired oscillations by averaging out the result by the period of that frequency:

\text{smoothed} \: \mathcal{F}\{\langle f(t) \rangle_a\}(\xi) = a \int_{\xi-1/2 a}^{\xi+1/2a} \mathcal{F}\{\langle f(t) \rangle_a\}(\xi_0) \, d \xi_0

The period of e^{-2 \pi i \xi a} is 1/a, so we modify the spectrum by taking the average with a window of that width at each point.

This is what the “smoothed” spectrum looks like for \langle \mathrm{sinc} \rangle_3, \langle \mathrm{sinc} \rangle_5, and \langle \mathrm{sinc} \rangle_{10}:

It tracks the original spectrum much more closely – in fact it’s useful to focus on the area around the cutoff to see what’s going on:

13. Deriving the Lánczos window would make this blog post too long and technical for my tastes. Lánczos himself derives it not by directly taking the inverse Fourier transform of the smoothed spectrum, but by adjusting the derivative of the error term.

    You can head to section IV.6 of Lánczos’ Applied Analysis for details. It is available for free at the Internet Archive.

    I also want to stress that Lánczos’ method for reducing the Gibbs phenomenon in truncated series is very general, and using it for interpolation together with \mathrm{sinc} is just one (very useful) application.↩︎

The plot above shows \mathrm{sinc}_3, the Lánczos window, and their pointwise multiplication. The spectrum is smoothed in exactly the way we desire. \mathrm{sinc} and its spectrum are also shown for reference.

While we set out to mimick \mathrm{sinc}’s spectrum, Lánczos interpolation actually works better than interpolating with \mathrm{sinc} in the presence of jump discontinuities, due to its dampened curve:

That said, a bit of ringing remains. This is the main drawback with Lánczos or similar filters, compared to linear interpolation or some cubic filters:

Nearest	\langle \mathrm{sinc} \rangle_3	\mathrm{Lanczos}_3

But for many applications, Lánczos (or something close to it) will be the best compromise.

Closing thoughts #

When I set out to write this post, I wanted to work up to Lánczos interpolation using just high-school maths. I couldn’t find a way to explain it without getting quite technical, so I downgraded to an explanation targetet to an audience who has at least heard of the Fourier transform.¹⁴ That said, I still hope this post could illuminate these key areas in modern engineering through a concrete example.

14. Yes, I’m talking to you, computer science undergraduate!↩︎

Cornelius Lánczos himself brought forward a multitude of numerical methods. I highly recommend “Applied Analysis”, the book that introduced the technique explained in this post. Some of it is outdated, explaining how to manually compute roots of polynomials or solutions to linear systems. It’s still very interesting, and written in an unusual conversational style that I find endearing.

Lánczos also strikes me as a delightful man, at least from two interviews I found on YouTube about mathematics and about his life.

Another reason to write this blog post was to showcase how much one can get out of software like Mathematica when playing around with such topics. In the end I mostly used Mathematica for plots, but I encourage you to look at the notebook to get a peek of what’s possible.

Acknowledgements #

Many thanks to Alex Appetiti, Alexandru Sçvortov, Alex Sayers, Stephen Lavelle, and Kurren Nischal for reviewing drafts of this blog post.