Here’s a suggestion about how we might replace Epigram’s datatypes by a universe of containers. It’s distinctly undercooked, but we’ll see how it goes. There are lots of design choices, so I’ll try to flag the issues.
We’ll be wanting some sort of
![\Rule{\vI,\vO\Hab\Type}
{\vI\blacktriangleright\vO\Hab\Type}
\quad
\Rule{\vD\Hab\vI\blacktriangleright\vO\quad
\vF\Hab\vI\to\Type\quad
\vo\Hab\vO}
{[\vD]\:\vF\:\vo\Hab\Type}](latexrender/pictures/019bff32a876a276d172bd611535443f.png "\Rule{\vI,\vO\Hab\Type}
{\vI\blacktriangleright\vO\Hab\Type}
\quad
\Rule{\vD\Hab\vI\blacktriangleright\vO\quad
\vF\Hab\vI\to\Type\quad
\vo\Hab\vO}
{[\vD]\:\vF\:\vo\Hab\Type}")
That is, we’re coding up dependent containers with given input and output sorts. Variations: we could use a sequence of input sorts, or just use sums; we could represent sorts by telescopes, rather than types. I suggest that both of these, although they require more work to set up, deliver functionality which is closer to what we actually want to use. But later…
The semantics is hardwired. It’s not an inductive definition, nor should it be. Moreover, I’m only giving the introduction behaviour here; the elimination behaviour will be peculiar, no doubt.
One base case delivers constant output
![\Rule
{\vo\Hab\vO}
{\DC{Out}\:\vo\Hab\vI\blacktriangleright\vO}
\quad
\Axiom{\DC{out} \Hab{} [\DC{Out}\:\vo]\:\vF\:\vo}](latexrender/pictures/8a5a38735c9e0062cc206cb0662bfc19.png "\Rule
{\vo\Hab\vO}
{\DC{Out}\:\vo\Hab\vI\blacktriangleright\vO}
\quad
\Axiom{\DC{out} \Hab{} [\DC{Out}\:\vo]\:\vF\:\vo}")
Meta: the blog software lets me colour ‘Out’ as you can see, but it turns ‘Output’ into [Unparseable or potentially dangerous latex formula. Error 2 ]. Methinks the ‘Never call anything z!’ bug strikes again. But I digress.
Another base case demands a specific sort of input, for any output.
![\Rule
{\vi\Hab\vI}
{\DC{In}\:\vi\Hab\vI\blacktriangleright\vO}
\quad
\Rule
{\vx\Hab\vF\:\vi}
{\DC{in}\:\vx\Hab[\DC{In}\:\vi]\:\vF\:\vo}](latexrender/pictures/60e9754d7ee428c720d1a294dd274f3b.png "\Rule
{\vi\Hab\vI}
{\DC{In}\:\vi\Hab\vI\blacktriangleright\vO}
\quad
\Rule
{\vx\Hab\vF\:\vi}
{\DC{in}\:\vx\Hab[\DC{In}\:\vi]\:\vF\:\vo}")
Containers chain up in sequence
![\Rule
{\vS\Hab\vI\blacktriangleright\vM\quad
\vT\Hab\vM\to\vI\blacktriangleright\vO}
{\DC{Seq}\:\vS\:\vT\Hab\vI\blacktriangleright\vO}
\quad
\Rule
{\vs\Hab[\vS]\:\vF\:\vm\quad
\vt\Hab[\vT\:\vm]\:\vF\:\vo}
{\DC{seq}\:\vs\:\vt\Hab [\DC{Seq}\:\vS\:\vT]\:\vF\:\vo}](latexrender/pictures/7f6bed068a07172265ef9bd4f19c5852.png "\Rule
{\vS\Hab\vI\blacktriangleright\vM\quad
\vT\Hab\vM\to\vI\blacktriangleright\vO}
{\DC{Seq}\:\vS\:\vT\Hab\vI\blacktriangleright\vO}
\quad
\Rule
{\vs\Hab[\vS]\:\vF\:\vm\quad
\vt\Hab[\vT\:\vm]\:\vF\:\vo}
{\DC{seq}\:\vs\:\vt\Hab [\DC{Seq}\:\vS\:\vT]\:\vF\:\vo}")
Er, um, some non-payload data (makes singletons!)
![\Rule
{\vX\Hab\Type}
{\DC{Arg}\:\vX\Hab\vI\blacktriangleright\vX}
\quad
\Rule
{\vx\Hab\vX}
{\DC{arg}\:\vx\Hab[\DC{Arg}\:\vX]\:\vF\:\vx}](latexrender/pictures/0b66bba1c4d6203b57d040ad80bd268d.png "\Rule
{\vX\Hab\Type}
{\DC{Arg}\:\vX\Hab\vI\blacktriangleright\vX}
\quad
\Rule
{\vx\Hab\vX}
{\DC{arg}\:\vx\Hab[\DC{Arg}\:\vX]\:\vF\:\vx}")
Better allow some higher order stuff (nothing negative, mind):
![\Rule
{\vT\Hab\vX\to\vI\blacktriangleright\vO}
{\DC{Pi}\:\vX\:\vT\Hab\vI\blacktriangleright\vO}
\quad
\Rule
{\vf\Hab\Pi\vx\hb\vX.\:[\vT\:\vx]\:\vF\:\vo}
{\DC{lam}\:\vf\Hab[\DC{Pi}\:\vX\:\vT]\:\vF\:\vo}](latexrender/pictures/de3b45f59b5352c3fd686bb88faaf33f.png "\Rule
{\vT\Hab\vX\to\vI\blacktriangleright\vO}
{\DC{Pi}\:\vX\:\vT\Hab\vI\blacktriangleright\vO}
\quad
\Rule
{\vf\Hab\Pi\vx\hb\vX.\:[\vT\:\vx]\:\vF\:\vo}
{\DC{lam}\:\vf\Hab[\DC{Pi}\:\vX\:\vT]\:\vF\:\vo}")
And let us have fixpoints
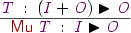
![\Rule
{\vt\Hab[\vT]\:
(\DC{inl}\:\vi\mapsto\vF\:i;\;\DC{inr}\:\vr\mapsto[\DC{Mu}\:\vT]\:\vF\:\vr)\:\vo}
{\DC{mu}\:\vt\Hab[\DC{Mu}\:\vT]\:\vF\:\vo}](latexrender/pictures/02ab8d28a9c5f70dd6320a9b15e93def.png "\Rule
{\vt\Hab[\vT]\:
(\DC{inl}\:\vi\mapsto\vF\:i;\;\DC{inr}\:\vr\mapsto[\DC{Mu}\:\vT]\:\vF\:\vr)\:\vo}
{\DC{mu}\:\vt\Hab[\DC{Mu}\:\vT]\:\vF\:\vo}")
similarly
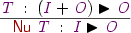
![\Rule
{\vt\Hab[\vT]\:
(\DC{inl}\:\vi\mapsto\vF\:i;\;\DC{inr}\:\vr\mapsto[\DC{Nu}\:\vT]\:\vF\:\vr)\:\vo}
{\DC{nu}\:\vt\Hab[\DC{Nu}\:\vT]\:\vF\:\vo}](latexrender/pictures/089acef817ce6493c32fadf5f937b0bb.png "\Rule
{\vt\Hab[\vT]\:
(\DC{inl}\:\vi\mapsto\vF\:i;\;\DC{inr}\:\vr\mapsto[\DC{Nu}\:\vT]\:\vF\:\vr)\:\vo}
{\DC{nu}\:\vt\Hab[\DC{Nu}\:\vT]\:\vF\:\vo}")
Is this enough? I bet we’ll also need composition, eg
\:\vo}
{\DC{comp}\:\vt\Hab[\DC{Comp}\:\vS\:\vT]\:\vF\:\vo}](latexrender/pictures/149f8ee6e9fae9490e9a5ea8f7709fe0.png "\Rule
{\vS\Hab\vJ\blacktriangleright\vO\quad
\vT\Hab\vI\blacktriangleright\vJ}
{\DC{Comp}\:\vS\:\vT\Hab\vI\blacktriangleright\vO}
\quad
\Rule
{\vt\Hab[\vS]([\vT]\:\vF)\:\vo}
{\DC{comp}\:\vt\Hab[\DC{Comp}\:\vS\:\vT]\:\vF\:\vo}")