November 13th, 2011
I’m still waiting for my computer to typecheck this file, which I concocted yesterday evening. I’m told by someone with a better computer (thanks, Darin) that it does typecheck, and moreover, satisfy the termination checker. It relies unexcitingly on the size-change principle and is easily rendered entirely structural.
What I’ve managed to do (at last!) is to implement an Agda model of Observational Type Theory for a hierarchy of universes, in this case Nat-indexed, but that’s probably not crucial. It’s a reasonably good fit with what we envisage for Epigram 2, once stratified. However, the real thing will not suffer all of the turd-transportation I just did to simulate cumulativity (the embedding of types from one universe into the next). Ouch, that hurt! It’s not pretty, but previously I didn’t know how to do it at all.
Let me try to explain what’s going on…
Read the rest of this entry »
Posted in General, Observational Type Theory | No Comments »
November 4th, 2011
Peter Morris is visiting Glasgow, so we’re trying to get on with writing an Epigram Elaborator. Let’s walk through the layers of the Epigram system.
- Evidence There’s an underlying type theory, the Language Of Verifiable Evidence. We have a bidirectional typechecker which means it can be quite compact, even though it is fully explicit. Necessarily, we also have a partial evaluator for it. LOVE will be total when we roll out the plan in Crude but Effective Stratification. There’s no need for a termination oracle: typechecking is the whole of the law.
- ProofState There’s a representation of incomplete constructions in LOVE: a hierarchy of longnamed definienda, some of which have lovely definienses (and are coloured green), but others of which remain ‘holes’ (coloured orange). Crucially, there is a mechanism for updating the ProofState with more informative types and values downscope of wherever an act of definition takes place.
- Cochon There’s an API for ProofState update which is a bit like an interactive theorem prover, with commands for making progress by refinement. We call it Cochon, as an homage. We even have a teletype-interaction wrapper for that API, which is what you currently have to put up with when you try out our prototype. We intend to preserve this system as a kind of ‘inspection hatch’ to the ProofState.
- The Elaborator is a robotic expert user of Cochon. Given a (possibly incomplete) lump of Epigram source code, the Elaborator will operate the controls of Cochon to perform the corresponding construction.
- The Transducer translates a textfile as a structured task for the Elaborator. When the Elaborator has finished, the transducer interprets the resulting ProofState as a patch to the original textfile, indicating the progress that has been made.
What makes it possible for the Transducer to generate readable patches from the bowels of the ProofState? How does the Elaborator know what to do? We follow James McKinna’s discipline of problems-as-types. LOVE gives types to the underlying semantic objects we care about, but it is also capable of wrapping those types in phantoms which also explain the problem intended to be solved by constructing a whatever-it-is. We have types not only for things, but for a-particular-thing-denoted-by-this-lump-of-source. We enrich types to capture the problems that the Elaborator must solve. Read the rest of this entry »
Posted in General | 4 Comments »
August 3rd, 2011
Where functional programs from my Dad’s thesis to ML and Haskell are given by sequences of equations and progress is made by matching patterns to determine which equation applies, Epigram is rather more explicit about the tree structure of problem refinement. (We may well get around to allowing the flattening of tree regions which just do ordinary case analysis, but the tree structure will not entirely disappear.) Correspondingly, a document is, morally, a block of components, where each component consists of one header line followed by a (possibly empty) subordinate block. It seems quite natural to allow (but not demand) that subordination be indicated by indentation.
Would that the world were wide, then layout would be easy. If the head line of a component is one physical line indented by n spaces, it should capture for its block either (i) the following {la; la; la} delimited by braces and semicolons, or (ii) all the contiguously subsequent lines indented by more than n spaces (blank lines are indented to ω). Let me show you what I mean, writing . for space and indicating subordination by longnames:
A
….A.A
……A.A.A
……A.A.B
..A.B
….A.B.A
….A.B.B
……A.B.B.A
…A.B.C
..A.C
B
Note that subordinate header lines can slide a little to the left as we go down: they need to be indented enough to be subordinate to the parent, but not so much that they become subordinate to an elder sibling. When header lines all occupy one physical line, the subordination is reassuringly geometric: you just trace upward from the left edge of the line’s text until you hit the interior of another line, and there’s your guv’nor.
The problem, of course, is that the world is not so wide. I’m a bit of an 80-column fogey, myself. If a header line is rather long, it’s nice to split it up into several physical lines, indenting all but the first. But that raises the key question of layout: how do you tell the difference between indented continuations of the header and the beginning of the block? Read the rest of this entry »
Posted in General | No Comments »
August 3rd, 2011
I wrote a lexer yesterday. It’s not very big.
slex1 :: Char -> String -> (STok, String)
slex1 c s =
case (elem c soloists, lookup c openers, lookup c closers) of
(True, _, _) -> (Solo c, s)
(_, Just b, _)
| (t, ‘|’ : u) < - span boring s -> (Open (b, Just t), u)
| otherwise -> (Open (b, Nothing), s)
(_, _, Just b) -> (Close (b, Nothing), s)
_ | c == ‘ ‘ -> let (t, u) = span (== ‘ ‘) s in (Spc (1 + length t), u)
_ | c == ‘|’ , (t, d : u) < - span boring s , Just b <- lookup d closers
-> (Close (b, Just t), u)
_ | c == ‘|’ -> (Solo c, s)
_ -> let (t, u) = span boring s in (Sym (c : t), u)
Let me translate that into something a bit more human. Read the rest of this entry »
Posted in General | 1 Comment »
August 1st, 2011
What should Epigram programs look like, as documents? When it comes to designing a source language of expressions and definitions, what choices must we make? Sooner or later, we need to choose a provisional syntax and get on with elaborating it.
This post is a collection of thoughts and worries, recording the state of my contemplation. Read the rest of this entry »
Posted in General | 2 Comments »
July 26th, 2011
The Epigram proof state is a collection of definitions in various states of repair. At any given time, it represents a snapshot in the process of elaborating a program in Epigram’s Source Language (which doesn’t really exist yet) into terms in Epigram’s Language Of Verifiable Evidence (perpetually in flux). In this post, I’ll try to sketch out the plan of the proof state and explain a bit about how elaboration sits on top.
Global Definitions
The basic idea is that the proof state is a sequence of global definitions, growing at the local end (a snoc-list, as it were), any of which may be a hole. Each definition gives a name either a ? or a known value (in the form of a term), and a type.
name = (?|term) : type
To check that a definition is ok with respect to a bunch of prior definitions, check that the type is a type, that the term (if given) has that type, and that the name is fresh. E.g.,
S = ? : Set
T = ? : S → Set
F = Π S T : Set
relies on the existence (but not any particular value) of S to ensure that T has a type; F’s value relies on both S and T.
Note that all definitions are in scope for subsequent definitions (but not for themselves — no recursion!) and that the equational theory of the new definition in scope is the obvious: she equals herself and also her value if she has one. We know that the type F, above, admits λ-abstractions, because she is, by definition, equal to a Π-type. Evaluation (to weak-head-normal form) expands definitions in head positions. Full normalization leaves only the holes. To make evaluation easier, share the whole definition with every reference: it’s the parser that looks up definitions, so the evaluator can just use their cached values.
Got the model of the snoc-list of definitions? Good, because the team didn’t quite implement it that way… Read the rest of this entry »
Posted in General | No Comments »
June 29th, 2011
Here’s the next episode in my story of algorithmic rules. I’m going to define a bidirectional type system and its definitional equality. Indeed, I’m going to define a bidirectional type system by its definitional equality. Read the rest of this entry »
Posted in General | No Comments »
June 29th, 2011
Sooner or later, it’ll be important to write down what it is we think we’re doing and try to prove some theorems about it. I’ve been thinking a bit about how to present systems of rules which are algorithmic, in the sense that relational judgments have distinguished input and output positions, where the inputs determine the outputs if the judgment holds at all. My first attempts just involved defining an inductive relation
R : S → T → Set
then laboriously proving, by induction of one and inversion of the other
R s t ∧ R s t’ ⇒ t ≡ t’
I had the nasty sensation of working too hard. In the systems I’ve been working with, information flows clockwise around the rules, from the inputs of the conclusion to the inputs of the first premise, … to the outputs of the last premise, to the outputs of the conclusion. This discipline ensures that we can turn the rules into a monadic program. So, thought I, why not do it the other way around? Write the program and extract the rules! Giddy-up-a-ding-dong!
Read the rest of this entry »
Posted in General | No Comments »
June 17th, 2011
James McKinna and I defined Epigram as a programming notation for the predicative fragment of Luo’s UTT, but I always dodged implementing the stratified hierarchy of universes, hacking in the (fun but) inconsistent Set : Set as a holding pattern. It’s not that I don’t care about consistency. It’s more that I’m unhappy with the pragmatics of many of the treatments I’ve seen and wanted to think a bit more about the problem. Now I think I have a little more to say.
The usual starting point is to consider a tower of ever-larger universes where each inhabits the next.
Set0 : Set1 : Set2 : …
Read the rest of this entry »
Posted in General | 2 Comments »
February 16th, 2011
So, we finally found some time to switch the term representation in the core, along the lines of Conor’s ‘Lower Taxation’ post (You can see the nucleus of this in the file ’src/Evidences/NewTm.lhs’). Correspondingly, we’re just about to break everything and then put it back together. This might take some time. If you want to play with the thing in the mean time we’ve tagged the current state of the repo – the magic incantations you’ll need are:
darcs {get,pull} –tag before-breakage http://www.e-pig.org/darcs/Pig09/
We’re off down the rabbit hole, see you at the other end.
Posted in General | No Comments »
December 20th, 2010
This post is another episode of the story of my latest term representation with its kit for legible working with de Bruijn indices. We can represent and evaluate terms: we had better make sure we can typecheck them.
What’s the type of the typechecker?
I’ll tell you, and name the inputs, so we can discuss them.
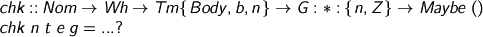
Where to begin...
Read the rest of this entry »
Posted in General | No Comments »
December 16th, 2010
Time for the next episode…
M’colleague Bob Atkey once memorably described the capacity to put up with de Bruijn indices as a Cylon detector, the kind of reverse Turing Test that the humans in Battlestar Galactica invent, the better to recognize one another by their common inadequacies. He had a point.
In this post, I’ll discuss some of the issues which have driven us to a de Bruijn indexed representation of values, where once we used Haskell functions to model Epigram functions. I’ll also introduce some technology which will hopefully make the resulting representation accessible to non-Cylons. It’s made possible exactly because our de Bruijn terms have a type indexed by the number of variables in scope.
Remember, folks, in the twenty-first century, the point of types isn’t the crap you’re not allowed to write, it’s the other crap you don’t want to bother figuring out.
Read the rest of this entry »
Posted in General | No Comments »
December 13th, 2010
A while ago, I was worrying about the term representation we use, and how much it was costing us. I’ve been thinking, and I’ve got a few ingredients. Let’s take a look at the terms, so far. (Yes, I’m using the Strathclyde Haskell Enhancement.)
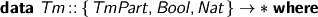
Terms are indexed by
- whether they may stand in the body of a term, or only at the head
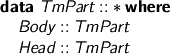
- whether they are weak-head-normal, or not
- how many de Bruijn variables are free
Bear in mind this special case: the closed weak-head-normal forms.
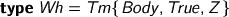
which demands that the term be ready for top-level inspection: you can match on a Wh and you know you can see what it means. You can’t accidentally forget to compute a term to weak-head-normal form and use it where a Wh is demanded. (But you can pattern match on a Tm, so care is still required.)
Read the rest of this entry »
Posted in General | No Comments »
September 10th, 2010
I’ve just managed to beat insertion sort into the system. It grumbles a bit, but it works. This is not Epigram 2 source code: it’s a Cochon script. Cochon is a low-level command-line interface to the Epigram 2 proof-state. Basically, you’re zippering around inside an unfinished hierarchical development, locally tinkering with this and that, incrementally solving the missing bits. But some Cochon commands are beginning to resemble a programming language.
Read the rest of this entry »
Posted in General | 3 Comments »
August 20th, 2010
Over the last few weeks, there have been some changes to Epigram that make programming in the command-line interface slightly more pleasant. We are starting to think about a high-level language, but in the meantime, I thought it would be nice to look at what sort of programming is possible today. None of this is revolutionary or indeed particularly exciting, but it should make the exciting stuff easier to write. This post would be literate Epigram if there was such a thing; as there isn’t, you will have to copy code lines one at a time into Pig if you want to follow along.
Read the rest of this entry »
Posted in General | No Comments »
May 31st, 2010
I think we’re at a point where we need to question our term/value representation technology. That’s not to say we need to change it, but we should look at where things are getting a bit out of hand and ask if there’s anything we can do. The system is not so large that…actually, it’s small. However, before we do anything foolish, I thought I’d try to remember where we’ve been and why. Please join in. We need to figure out what breaks what. Most representation choices have pros and cons (a few just have cons).
Where are we at the moment? Read the rest of this entry »
Posted in General | 3 Comments »
May 24th, 2010
Here’s a story I’ve had on the go for a while.
 It’s an experiment in managing the multitudinous variations on the theme of a datatype, inspired by this overlay from a talk I gave ten years ago. If you squint hard at it, you can see that it shows the difference between lists and vectors. Let’s see how to formalize that notion as a big pile of Agda. The plan, of course, is to do something very like this for real on Epigram’s built in universe of datatypes.
It’s an experiment in managing the multitudinous variations on the theme of a datatype, inspired by this overlay from a talk I gave ten years ago. If you squint hard at it, you can see that it shows the difference between lists and vectors. Let’s see how to formalize that notion as a big pile of Agda. The plan, of course, is to do something very like this for real on Epigram’s built in universe of datatypes.
I’ll need some bits and bobs like Sigma-types (Sg). Step one. Build yourself a little language describing indexed functors.
Descriptions
data Desc (I : Set) : Set1 where
say : I -> Desc I
sg : (S : Set)(D : S -> Desc I) -> Desc I
ask_*_ : I -> Desc I -> Desc I
What do these things mean?
[_] : forall {I} -> Desc I -> (I -> Set) -> (I -> Set)
[ say i' ] X i = i' == i
[ sg S D ] X i = Sg S \ s -> [ D s ] X i
[ ask i' * D ] X i = X i' * [ D ] X i
Here, [ D ] X i is the set of D-described data which say they have index i; everywhere the description asks for some index i’, the corresponding set has an X i’. Meanwhile sg just codes for ordinary Sg-types, allowing nodes of datatypes to be built like dependent records. The X marks the spot for recursive data. Our next move is to take a fixpoint.
data Data {I : Set}(D : Desc I)(i : I) : Set where
<_> : [ D ] (Data D) i -> Data D i
I guess I’d better give you an example. Read the rest of this entry »
Posted in General | No Comments »
May 10th, 2010
In this post, I talk about the computation of normal forms in Epigram. Quotation is a key step of normalization, doing some rather exciting magic.
Setting the scene
This post tells a story about terms. We shall discover that some classes of term are more desirable than others. Let us have a look at the battlefield. We define 3 classes of terms, gently sketched by Bosch:
Read the rest of this entry »
Posted in General | 7 Comments »
April 24th, 2010
I thought I would write a line or two about some recently acquired infrastructure.
Weeks ago, we had left our ivory tower, or rather, our beloved Livingstone tower for a gig in Oxford. Lot of fun, lot of adjunctions. But also a surprising discovery: we met some people who had pulled Epigram source code and actually looked at it. I mean, I might have pulled the code once or twice in the past, to impress girls in a Pub. But reading it…
Worse, we actually got our first bug report! Andrea Vezzosi, as a modern Dante Alighieri, braved the Inferno of She-ism (translates to “shitism” in Italian for some reason) and somehow went through the Purgatorio of Epigram’s syntax (honestly, I have no clue how he did that). Once there, Paradiso was at hand. But these damned labels were preventing the magic from happening! No mailing list, no bug tracker: no hope.
Around the same time, our counter-intelligence team reported that several Epigram agents under cover in Sweden had been busted and exposed to bursts of .45mm questions.
All in all, we came to the conclusion that, out there, there are people working harder on Epigram than we do. So, here is the kit for you to become an Epigram implementor:
If you don’t feel like becoming a modern hero (tough job, indeed), you are also welcome to come on board and have a chat with the captain.
I’m putting a rough skeleton of my PhD thesis in the repository. I’m off to Honolulu, will be back in 3 years. Keep up the good work folks!
Posted in General | No Comments »
April 18th, 2010
Let me try to make a bit of high-level sense about Prop in Epigram 2. It’s quite different from Prop in Coq, it does a different job, and it sits in quite a delicate niche.
Firstly, Prop is explicitly a subuniverse of Set. If P is a Prop, then :- P is the set of its proofs, but P itself is not a type. (Are propositions types? How, functionally, should the Curry-Howard “isomorphism” be manifest?) Note that :- is a canonical set constructor; it is preserved by computation. Hence you know a proof set when you see one.
Secondly, we squash proof sets. All inhabitants of proof sets are considered equal, definitionally. We have that :- P ∋ p ≡ p’, and we can easily see when this rule applies, just because :- is canonical. Contrast this with Coq, where Prop is silently embedded in Type: that makes it harder to spot opportunities to squash proofs.
And that’s kind of it. Prop is a subuniverse of Set that’s safe to squash, even when computing with open terms. There’s nothing we do with Prop that we couldn’t do more clunkily in Set. It is, in effect, an optimization. However, the pragmatic impact of this optimization is considerable. More on what we’ve bought in a bit; let’s check that we can afford it.
Read the rest of this entry »
Posted in General | No Comments »
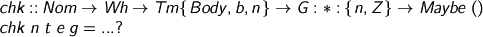
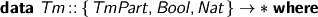
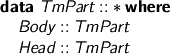
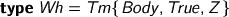
 It’s an experiment in managing the multitudinous variations on the theme of a datatype, inspired by this overlay from a talk I gave ten years ago. If you squint hard at it, you can see that it shows the difference between lists and vectors. Let’s see how to formalize that notion as a big pile of Agda. The plan, of course, is to do something very like this for real on Epigram’s built in universe of datatypes.
It’s an experiment in managing the multitudinous variations on the theme of a datatype, inspired by this overlay from a talk I gave ten years ago. If you squint hard at it, you can see that it shows the difference between lists and vectors. Let’s see how to formalize that notion as a big pile of Agda. The plan, of course, is to do something very like this for real on Epigram’s built in universe of datatypes.