In this post, I talk about the computation of normal forms in Epigram. Quotation is a key step of normalization, doing some rather exciting magic.
Setting the scene
This post tells a story about terms. We shall discover that some classes of term are more desirable than others. Let us have a look at the battlefield. We define 3 classes of terms, gently sketched by Bosch:
The Garden of Earthly Delights (courtesy Wikimedia)
Terms in Hell
On the right panel, we have terms, any kind of terms: the sinful Y, the depraved Omega, as well as many non-sensical objects. In this land of fear and misery, things can go wrong, badly wrong. If you’re doing a PhD, you’re likely to live in there.
Values on Earth
In Epigram, well-typed terms are strongly normalizing (forget set-in-set, forget set-in-set, forget set-in-set,…): evaluation of well-typed terms terminates, reaching a normal form. So, provided that they are well-typed, we can save some souls from Hell by evaluating them:
- Applying β-reduction, ie.
![(\lambda x . t) s \leadsto t[x/s]](latexrender/pictures/7e56859818c425e5234c6af779eed622.png "(\lambda x . t) s \leadsto t[x/s]")
but also projections on pairs (σ-rules), elimination over datatypes (ι-rule), etc. - Applying δ-reduction, ie. expanding definitions
And we get βδ-normal forms, rather naturally called values, i.e. the result of (untyped) evaluation. Definitional equality could be implemented as follow. Terms are reduced to values and syntactically compared. If they match on the nose, win. Otherwise, prove.
Normal forms in Eden
Is this the end of story? Well, what does our customers want? They want a powerful definitional equality: less silly proof obligations! However, much as a British MP, we need to be careful in our promises, or we will end up with a “hung type-checker”. Indeed, definitional equality needs to be decidable if we want type-checking to be terminating. That’s where the cautious quotation comes into play.
Quotation, putting types at work
When computing βδ-normal forms, we simply evaluate terms, without using type information. In the dependently-typed world, ignoring types is a major sin. Types are here, they have something to say! Let’s listen to them!
η-expansion for free
So, we join the Normalization by Evaluation crew: we reify values from Earth to normal forms in Eden. As a first step, let us have η-expansion to hold definitionally, that is:
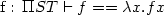
Or:
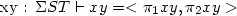
For example.
We consider a small ΠΣ language, with the expected static and dynamic semantics. Because it’s so damn useful, we adopt a bi-directional presentation: types are pushed in or pulled from terms. This story has been told in many places, including Sweden. I won’t recall the type system, but I can be convinced to do so.
We define quotation, pushed and pulled, by the following judgements:
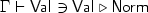
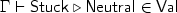
Where “Val” and “Norm” are different syntactic categories, namely values and normal forms. “Stuck” is a subset of normal forms, while “Neutral” is a subset of values. The jugdement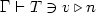 
reads as “the value v of type T is quoted as n“. The judgement 
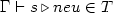reads as “the stuck term s is quoted as neu and, by the way, its type is T.
Let us start with the “pull” side. There is little to be done there: we bureaucratically get the type out of where-we-can and proceed structurally. That is:
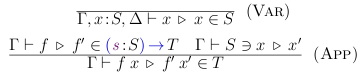
Then, we can move from the “pull” side to the “push” side by a kind of conversion rule (remember, type-checking already happened, so this is safe not to check for equality of S and T):
The quotation of canonical inhabitants of Set is not exciting either. It’s structural and bureaucratic:
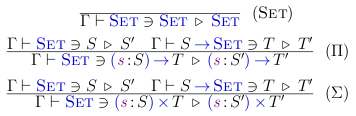
Ok, now for something exciting, at last. Quoting functions and pairs:
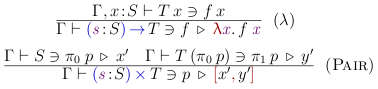
The quoted function is an η-expanded function, while the quoted pair is really a pair of the projected components. Therefore, we achieve our goal above. This quotation mechanism gives us βδ-normal η-long forms.
In real life, these rules are implemented in Evidences/Rules.lhs by the mutually-recursive functions inQuote and exQuote. They are called upon by quote that implements the conversion rule.
All of this is not new: Agda supports it, as described in Ulf’s PhD thesis.
I want my functor laws, my monad laws, and a Parliament. Please.
Let us look at an example. I assume that you’re familiar with Epigram’s universe of datatypes (I can easily be convinced to write a post on that, if necessary). For simplicity, I will consider the universe of simple inductive types, Desc. In a sense, we can see it as a language for describing endofunctors on Set.
Wait, functor? So, there is a morphism part? Yes, there is one, call it map. It satisfies the well-known functor laws:
Now, imagine that x is a neutral term (it cannot compute further). Because x is stuck, the whole 
is stuck as well. That’s a bit silly because we know that, whatever x might be, is really nothing but x.
Well, we simply have to extend the quotation machinery to catch that. In our gang, this is known as Boutillier’s trick. I’m told that in Royal Holloway, this is called χ-normalization (Adams and Luo). So it goes:
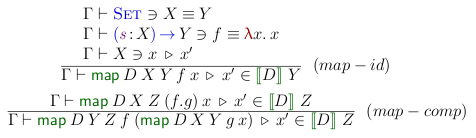
Note that a simplification can cascade into further simplifications. Let us consider swap : Sig (A; B;) → Sig (B; A;). What do you think happens on map swap (map swap l)? Well, we apply (map-comp), so we try to simplify map (swap . swap) l. Oh but swap . swap, that’s id. Thus, (map-id) triggers and gives us l. Definitionally. (See ./test/MapSimp.pig and ./test/OpSimp.pig)
That was for functors. Now, you probably know that Desc (and, more interestingly, IDesc) enjoy a free monad structure. Well, same story: we can make monad laws hold definitionally. (See ./test/FreeMonad.pig). The term we obtain through this extended quotation is in βδχ-normal η-long form.
I know what you’re dreaming of: plugging these simplification laws as you define “new stuffs”. Well, we have to be careful there: the simplification on stuck term must really behave exactly the same way than the normal (computational) behavior on non stuck terms. I, personally, don’t know how to ensure these things and inform the type-checker that some simplifications are “safe”.
What about Prop?
Yes, indeed. The whole point of this post was to answer Russell’s question. If I don’t want to run out of work, I’m better off not answering the question this time. That’s the first lesson of Job Security 101. Stay tuned ;-)
To sum up today’s lesson, a picture is worth a 1208 words:
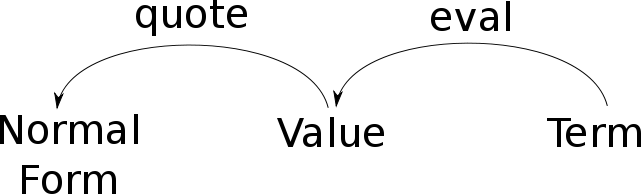
Where a term is anything you want, a value is a βδ-normal term, and a normal form is a βδχ-norm η-long form.
Further references
This story has been told in more details in a report by Pierre Boutillier.
As for NBE, I would recommend the seminal paper by Dybjer and Filinski. In the dependently-typed world, my favorite is James’ PhD thesis, but I’m biased.
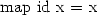
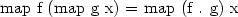
/me raises his hand for a question
Looking at map-id, is there a case where
\Gamma |- (s:X) -> Y \ni f == \x -> x
would hold
\Gamma |- Set \ni X == Y
wouldn’t ?
(btw, it seems you forgot to adjust the type of the result in App)
The problem is that what is on the left of the \ni is the thing we trust. When you are checking f for equality with λ x . x, you really need to type-check it in X → X. So, you need to ensure that X == Y, so that (s : X) → Y is X → X. You don’t want to put lies on the left of the \ni. Does that make sense?
Thanks for the App, that’s indeed a typo.
I see Pierre-Évariste has beaten me to it. Let me fill in a bit of the background.
We try to write presentations of rules which give rise directly to the appropriate algorithms. Each judgment form has input positions and output positions, preconditions explaining our requirements of inputs, and postconditions giving guarantees about outputs.
In the case of Γ |- T ∋ u == v, all four positions are inputs. The preconditions are Γ |- T ∋ t and Γ |- T ∋ v. That is, to ask if two values are equal at type T, you must first know that they both have that type.
How do we use rules? We work from conclusions to premises. We may presume that the conclusion preconditions hold (or we would not be interested in the problem); we may reduce the conclusion to a collection of premises only if we can establish their preconditions, left-to-right.
Hence, indeed, we have to check that X is Y before we may ask if f is id.
Thanks, it’s clear now, the implicitness of the precondition tripped me up.
What kind of simplification is possible with regard to eliminators? For instance, if you don’t do any, then despite having:
f == \x -> x ==> map f x == x
Some identities are more equal than others. For instance, what if:
f = \n -> elim_Nat Z (\_ -> S) n
I guess this is more eta, so does \x -> x get expanded into the version with the eliminator (sums are part of why eta expansion is preferred, as I recall). Or does one try to recognize eliminators that just rebuild the thing they’re eliminating?
We do eta-expansion only for Pi and Sigma, and (the as yet underexposed) proof-squashing. We currently make no attempt to rearrange stuck inductive eliminators: commuting conversions are a tricky business even for sums, let alone recursive types. I’m too scared to get in with those alligators.
So, yes, (inevitably, of course), some identity functions are more equal than others. The quotation rules for map (and one or two other things) exploit structure which is present by construction. We aren’t really used to this technology yet: it certainly has many more possibilities, but we haven’t yet got a feel for what we can/should do. Interesting times. (There’s a free indexed monad just around the corner.)
It occurred to me somewhat later that one can write two different identities with the usual eliminator for naturals:
elim_Nat Z (\n r -> S n)
elim_Nat Z (\n r -> S r)
So doing either expansion is going to leave something out, and can’t work, I suppose. Perhaps there is hope for reduction, though. As I recall, the issue with eta reduction is that it breaks confluence and uniqueness of normal forms. However, if you’re already at beta-normal forms before doing any quotation, it presumably doesn’t matter whether some non-normal term has both beta and eta redices that lead to irreconcilable terms; only beta can happen at that point.
That of course says nothing about whether detecting identity eliminations is feasible.