Issues and Inklings

This page is intended to be common property, a collection point for issues which Epigram might benefit from addressing and inklings as to how we might address them.

Datatypes

  • Locally defined datatypes
  • Coinductive datatypes
  • Mutual datatypes (including mixed induction and coinduction)
  • Induction-recursion
  • Mutual telescopes of datatypes

But it’s not just a question of which datatypes we’re allowed, there’s also room for improvement in the generation of datatypes.

  • Datatypes in a universe
  • Refinements of datatypes
  • Datatypes generated for reflection, defunctionalisation, collection of unfinished cases
  • Refactorings of datatypes

Interested individuals should look out for authors such as Peter Dybjer and Anton Setzer, as well as our own Nottingham Container Consortium (Altenkirch, Ghani, Hancock, McBride, Morris, Swierstra, insert your name here).

Computations

Life’s no fun without a little impurity here and there. Haskell’s monads are all jolly well, but there’s so much more waiting to be found. We get to think it out again. I’d like to see a situation where more syntax is spent on establishing which effects are locally available and less on plumbing effects through expressions. Half an idea: work with respect to a local ‘notion of computation’; spend syntax on shifting aspects of computation between explicit types and the ambient notion; retain the ordinary syntax of expressions but allow locally sanctioned effects. Turn ‘do’ back into ‘let’!

Source materials are numerous and diverse. In terms of representing the underlying phenomena, Peter Hancock’s work is a good place to look: crucially, he has studied the incorporation of notions of ‘state’ in the types of interactive processes, thus controlling the functionality available statically in a way which is properly reflects what happens dynamically. Meanwhile, work by John Hughes (arrows), Tarmo Uustalu and Varmo Vene (comonadic programming) and myself and Ross Paterson (applicative functors, aka idioms) provide good evidence that an excessive fixation on monads is unhealthy, something John Power hs been telling people for years.

Stratisfaction

is not the abstract noun from the verb ‘to stratify’, but it should be. This \star:\star lark can’t go on. There are two popular approaches to universe stratification, which Martin-Löf refers to genderbendingly as ‘à la Russell’ and ‘à la Tarski’. The Russell style (as in Coq and Lego) supports implicit cumulativity, with both \star_0:\star_1:\star_2:\ldots and \star_0\subset\star_1\subset\star_2\subset\ldots. 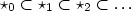The Tarski style is more explicit, with a names-and-decoder presentation of each universe: the level n types have names belonging to a level (n+1) type, with the names decoding to the types; there’s an explicit embedding function between level n names and level (n+1) names; individual levels are closed under Π-formation, etc.

The latter seems a better basis for level-polymorphism. It’s important to be able to say that every level is closed under List, not just that some level is closed under List (as you would find in Lego, Coq, Cayenne,…). It strikes me that a good candidate for stratification in the core theory is to have a Tarski-like system with implicit decoding (types are their own names) but with explicit lifting and straightforward let-polymorphism. Note that the appropriate treatment of datatypes should follow directly from the treatment of definitions in Epigram 2, now that we introduce datatypes via a universe anyway.

How all this should be made manifest in the source language remains an open design problem which I occasionally snatch a moment to think about. But I see it more as a decent-sized chunk of someone else’s PhD. Interested individuals should check out key related work by Bob Harper and Randy Pollack, Judicaël Courant, Zhaohui Luo and Paul Callaghan.