This post is another episode of the story of my latest term representation with its kit for legible working with de Bruijn indices. We can represent and evaluate terms: we had better make sure we can typecheck them.
What’s the type of the typechecker?
I’ll tell you, and name the inputs, so we can discuss them.
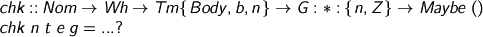
Where to begin...
What type are we checking? Type t. Note that we trust this t to belong to some sort already: it is not the subject of the enquiry. Moreover you (and GHC) can see that t is in weak-head-normal form. If t is equal to a canonical set (Set i, Π, Σ, 1), it will have a canonical set constructor. We can pattern match (one level deep) with confidence that we’re not getting false negatives through failure to compute. We’re further obliged to maintain these invariants as we push types inward, recursively.
What are we checking has this type? Expression e, which is a general Body form. The structure of the process is bidirectional: we check the types of Body terms and infer the types of Head terms, then propagate type information from heads along spines. Where we have two types, we check that the inferred type fits inside the checked type. Sometimes we have no type (when the term is not β-normal), and there we compute to a form we can typecheck.
Computation before typechecking is worrisome: the point of typechecking is to ensure safe computation. User-constructed terms contain no β-redexes, and any environments cached in binding operators are always Nil. We shall thus be able to ensure that no part of such a term is computed until it is checked. I could enforce this invariant more tightly, either statically by an extra index on Tm characterizing user-constructability, or dynamically by signalling an error when the wrong sort of term turns up. Here, I just compute β-redexes out to a form I can check: β-redexes in terms are created by the kernel, so should not actually need checked (perhaps the checker should just say yes!) but I can imagine using the checker to test for bugs. The given implementation sustains such paranoia.
Now, you can see from its type that e has free de Bruijn variables. Our de Bruijn variables are not typed, nor can we use them to make weak-head-normal forms. Correspondingly, we can only cope if we have an environment to interpret them. In normal usage, we expect the environment g to map the dangling untyped de Bruijn V-variables to inert, free, typed R-declarations. In more formal presentations, it is traditional to substitute free-for-bound when one goes under a binder: here, the environment accumulates those substitutions and they’re applied just-in-time.
So, barring the environmental indirection, it’s the usual plan, and we do need to generate a fresh declaration when we go under a binder. That’s what n the Nom is for. (I’m not sure why I always name that type in French (as opposed to Latin or Lolspeak), but it’s an old and comforting habit.) The operation nxt :: Nom -> Nom maps a fresh name to an even fresher name. Leastways, it is vital to ensure that no amount of nxt-ing can ever cause a clash with a name that’s been passed in. The capacity to split the namespace into orthogonal chunks is crucial here, but that’s an old old story… In my toy checker, I’m taking Nom = (String, Int) and nxt incrementing the Int: reserving a string (e.g. “”) for the typechecker’s use will get us all the freshness we need.
References Reviewed
As we’ll need to generate fresh references, let’s just remember what they consist of. They’re either declarations or definitions, and the Boolean index tells you whether they’re allowed at the head of a Wh or not.
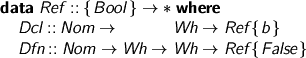
Equality for references is nominal. Correspondingly, we really must not screw up the freshness management. We often need to get a reference’s vital statistics.
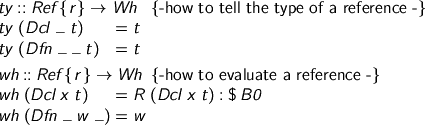
We also need to make declarations. Here’s how,
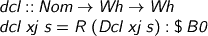
And with that, we’re pretty much ready for the off.
Checking the Canonical
Checking sorts is level comparison.
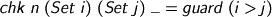
Checking Π and Σ follows the procedure: check the domain, declare a fresh variable in the domain, check the range.
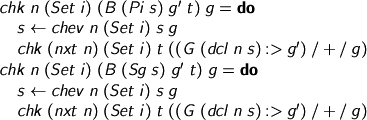
Oh, I forgot to mention the handy check-then-evaluate gadget.
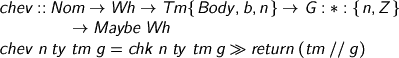
Notable things. In normal usage, we are sure that g’ (the environment cached by the binder during evaluation) will be empty, but we glue it onto the typechecking environment anyway (as we must, if we are to work in the correct scope for the range). Note also that I shadow the raw input domain s by its checked value, making doubly sure I don’t misuse the old version. I say doubly, because the raw s is conspicuously in the wrong scope to be used as the type of a declaration and GHC pulls me up when I accidentally forget (which is easily done). Once we’ve got the domain type, we bung a fresh declaration into the environment. That’s the only way the typechecker ever constructs a context extension, so for normal usage, the environment is indeed just a bound-V-to-free-R renaming.
Oh yeah, lest we forget:
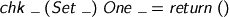
Moving to the value-formers, let’s have λ
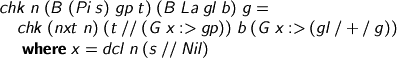
We don’t need a type annotation on λ because we’re always checking against the Π, so we have a type for the dummy argument. We declare and go under. Note that although the domain s is V-closed, it is not necessarily weak-head-normal, hence dcl n (s // Nil) typechecks where dcl n s would not! You can also see that it’s environments a-go-go, but their scope-indexed types mean GHC won’t let you muddle them up. In normal usage, gl comes from the user and is Nil, but gp lives inside the kernel and may very well not be.
For pairs, we check componentwise. Note how we need the value of the first to complete the environment in which we evaluate the type of the second.
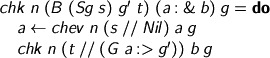
And, of course,
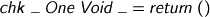
After that, things get slightly weirder.
Closures, Heads, Spines
We have several cases still to cover. If we encounter a closure (and we’ll see why we might in a moment), we just unpack the environment and carry on.
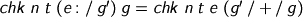
If we’re lucky enough to find an applied reference, we change direction!
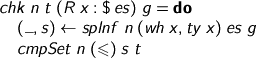
Whether declared or defined, we can read ty x, the type of the reference, then work our way along the spine to compute the type s of the whole term. We must then make sure s is included in t. The cmpSet operation must wait a little, but let's look at spines now.
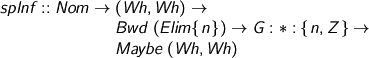
We need a name supply. We need the value (why?) and type of the term being eliminated by the spine. Given the spine and its shared environment, we should (if lucky) be able to reconstruct the value and type of the whole elimination. If the spine is empty, we’re lucky.
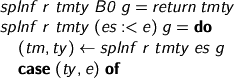
If not, we split the spine into its torso and tailpiece and check the torso. The value and type we get back will tell us how to check that tailpiece.
If we get a function type, we should hope that the tailpiece is an application. We check that the argument is accepted by the domainand evaluate it, allowing us to generate the value and type of the application.
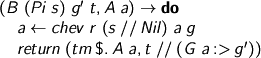
Note that ($.) is a convenient infix form of elimination for weak-head-normal forms. See the earlier post for the definition of elim.
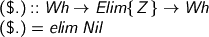
Meanwhile, for pairs we have projections. These are easy to check. Note that we need the value of the first projection to give the type of the second, and that is why spInf needs the value being eliminated as well as the type. Strong existentials, what are they like?
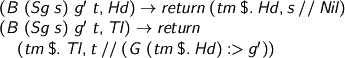
Any other tailpiece at any other type, and we’re done for.
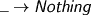
Bound Variables and Other Stories
Back in chk, what if the head applied to a spine isn’t a reference? Let’s see…
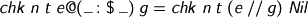
I say compute and go again! This is pretty much all we can do if the head is some random value embedded during computation. However, this case also kicks in when the head is a bound V-variable. Why is this ok in normal usage for a user-supplied term?
Inertia. If we are checking something like (V i :$ (B0 :< A a1 :< ... :< A an)), it's perfectly safe to weak-head-normalise, provided the environment g maps V i to some R xi.
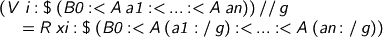
Phew! The arguments are not evaluated, just turned into closures. We check the result of the computation, we find the correct reference, spInf distributes argument types, and chk unpacks the closures, checking each argument in its appropriate environment.
Any typechecking problem which remains uncovered is a goner.
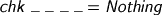
An Uplifting Thought Experiment
When is a value in type s usable at type t? Now that I’ve added universe levels, that ain’t quite the same question as is s t? Or is it? It depends on how we handle the shifting of types between levels. (Agda fans: I’m not sure exactly what Agda does here, but I know it’s less than you want.) We could add some explicit syntax to shunt stuff up a level. Would it be a canonical constructor? I think that’s basically what you can do in Agda. You get to pack and unpack (hopefully with η laws, so you don’t get hung up on bureaucracy, even if you have to do it).
But how about we make it an eliminator? We could add Up :: Elim {n}, with X Up living in Set (n+1) if X lives in Set n. Correspondingly, we’d need to explain how Up computes for canonical sets. We can just do that structurally. Note that (Set i) Up is (Set i), because Up moves our point of view up — the thing itself stays where it is. On canonical sets, Up does nothing! By the way, that’s a consequence of the bidirectional approach: canonical set-formers don’t need to say which level they’re working at, because they get told! If they had level annotations, Up would need to adjust them.
So where does Up end up? In clumps at the end of spines. The only thing you can eliminate an Up with is another Up. An Up-clump of length j at the end of a spine just shifts the Set i we’ve got up to the Set (i + j). If the Up-clump was missing, we could just compare the levels.
Meanwhile, how should we compare two spines which end with Up-clumps for equality? Is (X Up) the same as X? Given that Up is just meant to shift viewpoint, not meaning, it really should be, and we can’t persuade them apart by any canonical candidate for X, as Up would just compute through. Can we ever find ourselves comparing (X Up) with X? Possibly. We have no guarantee that spInf will compute a type at the same level as the type chk demands. We need type comparison to be viewpoint-level-heterogeneous. Concretely, the polymorphic identity function will have Set 1 type (X : Set 0) -> X Up -> X Up. If we apply it to some y : Y, we will get an element of Y up, which needs to go wherever a Y can.
So, for this theory as it stands, Up serves only as a source of obfuscation, ignored in equality and replaceable by a level comparison wherever a low level is embedded into a higher level. We can get rid of Up and implement cumulativity of levels silently.
Remark. Silent cumulativity is a kind of subtyping, and if you are not scared of subtyping, you have not properly understood it. Here, in our rather explicit system, our constraints are inequations on known constants and easily checked. If we turn things around, so we’re trying to infer levels in which we’re polymorphic, we can quickly rack up much harder constraint problems, and we run the risk of underconstrained systems leading to ambiguities. One can try to make sensible default choices, but in incremental construction environments, default choices can cease to be sensible in the light of newly arrived information. Perhaps I’m hopelessly naïve, but I’d like to see how far one can get with elaboration making the minimal commitments. As more degrees of freedom are added, making Up explicit may be the least bad option in avoiding underconstraint.
For now, though, let us enjoy the luxury of certainty.
Cumulativty and Equality
Set comparison takes a name supply, a comparator for universe levels, and two sets to be compared. Here’s where the comparator bites.
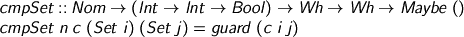
Comparison for Π-sets is contra/co in the components. It’s a bit fiddly.
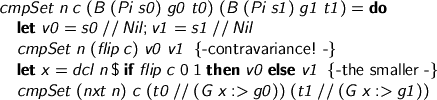
When we’re checking if (x : S0) -> T0 embeds in (x : S1) -> T1, we need to check that an S1 goes wherever an S0 is needed, and that a T0 goes wherever a T1 is needed, but we must check the latter with some x in scope. We pick x : S1, because it goes wherever an S0 is needed, but the other way around is not necessarily the case.
Incidentally, pushing cumulativity componentwise through canonical types isn’t vital. It’s certainly not required to simulate the checking of explicit Up, after we’ve erased them all. But in the explicit system, if F : Set1 -> Set1 and you want to use it at Set0 -> Set2, you have to write λX. F (X Up) Up, Up-adorning an η-expansion of F. While that would not be such a cruel fate, I think we can avoid it. To see this, consider how to embellish cmpSet so that it computes the number of Ups to insert — when we go under a binder, we bind at the smaller type, then add Up as needed to use that bound variable at the larger type.
The Σ case is covariant in both components.
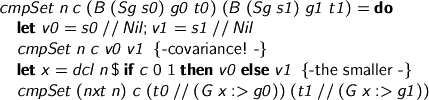
Finishing the comparator, we have the basics
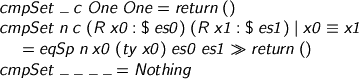
One is oneself. Neutrals (applied variables) are compared on the nose. All else fails.
From here on in, life’s a beach. We have a type-reconstructing equality for spines (with a shared head). You need the type from the shared prefix to see how to compare the tailpieces.
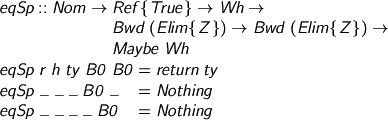
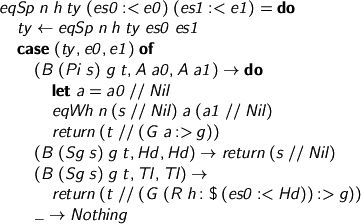
Remark. This practice of zipping spines together is fine for now, but as the theory grows, there’s something to remember. We must never have a proof-relevant eliminator for a proof-irrelevant type. You see the problem? If we’re comparing x rhubarb custard with y crumble custard, we would be wrong to say no if x rhubarb and y crumble have a proof-irrelevant type. We must ensure that any such custard leaves us still at a proof-irrelevant type (in which case, we never call the test in the first place). Say no to lumpy custard. Absurdity elimination and coercion between equal sets are proof-relevant operations on proof-irrelevant sets: we can add them (how is for another time) but not as eliminators.
Last but not least, the type-directed equality for weak-head-normal forms, taking a name supply, a type and two values of that type.
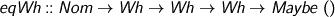
Given that we’re comparing set arguments to unknown functions, we had best check on the nose.
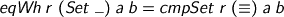
Somehow, that’s appropriate for comparing sets-as-values, rather than the looser requirements for compatibility at a particular usage. I wonder also if I smell a value-computation distinction, but that really is another story and not one I know just now.
The unit type is proof-irrelevant (no eliminators, no problem).

To compare functions, apply them to a fresh dummy argument. Effectively, η-expand on the fly.
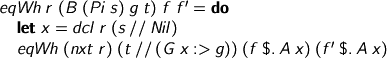
Similarly, pairs are checked componentwise.
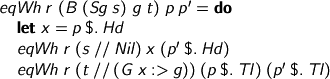
Otherwise it’s zippable spines…
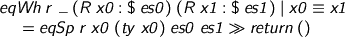
…or bust.

Phew!
We made it! The code is here.
So, what have we? A new representation for terms which lets us enforce weak-head-normality if we want, an evaluator, a typechecker, and an equality test. We have a system with cumulative universes. We implemented neither substitution (delayed by use of environments) nor quotation (built into equality, but not needed just to get values into first-order representation). Who knows? We might be able to cope with something like this. Let’s see in the weeks to come…