A while ago, I was worrying about the term representation we use, and how much it was costing us. I’ve been thinking, and I’ve got a few ingredients. Let’s take a look at the terms, so far. (Yes, I’m using the Strathclyde Haskell Enhancement.)
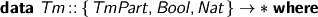
Terms are indexed by
- whether they may stand in the body of a term, or only at the head
- whether they are weak-head-normal, or not
- how many de Bruijn variables are free
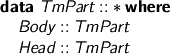
Bear in mind this special case: the closed weak-head-normal forms.
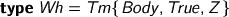
which demands that the term be ready for top-level inspection: you can match on a Wh and you know you can see what it means. You can’t accidentally forget to compute a term to weak-head-normal form and use it where a Wh is demanded. (But you can pattern match on a Tm, so care is still required.)
Back to the terms…
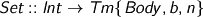
This time, it’s stratified! Now, mind this: Set is available whether or not the term is supposed to be weak, and however many binders we’re under. The indices represent requirements, not measurements.
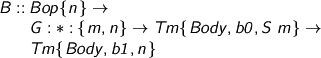
OK, this is where it gets a bit peculiar. B is for bind, starting with n free variables. Bop {n} is the type of binders available (Π and Σ with domain annotations, λ without).
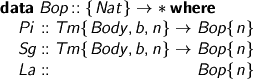
The body of the binder is not obliged to be head normal (it’s not at the head!) and it’s got {S m} (at least one) free variables. Between {m} and {n}, there’s an environment, which can be (and often is) Nil, making m=n. Including an environment allows us to suspend the execution of a function until its argument turns up.
Next, the unit type, pairs and void. Not much to see here
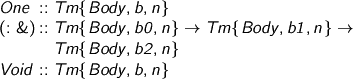
So far, it’s all been intro forms. Of course, there should be more features, but that’s enough to get the idea. Meanwhile, how do you do anything? I’ve used a spine representation, rather than a type of neutral terms. Why? I want immediate access to the head, so I can see if there’s a redex. A spine is a backward list of eliminators — backwards so we can easily stick more on the end.
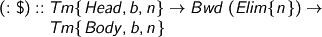
I’ll get to heads in a moment. Here, spines are made of applications and projections.
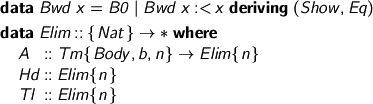
Now, here’s a possibility we didn’t have before. As long as you’re not obliged to produce a head-normal form, why shouldn’t you have a closure? We can choose to suspend evaluation outside of head position.
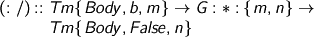
At the head of a spine, you can’t have anything you like, but hopefully you can have what you need: free variables, bound variables and… weak-head-normal forms?
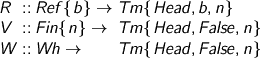
Er, um, check this first: a free variable is a context reference, either a declaration or a definition. Both carry a type, but a definition also has a value and is definitely not weak-head-normal.
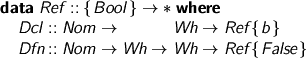
Neither is a bound variable weak-head-normal (for it must be looked up in the environment). Meanwhile, if you’re implementing an operator which gets a bunch of Wh values and has to compute something, you’d want to be able to do stuff with those values: as long as you don’t claim you’re making a weak-head-normal form, you can.
Let’s get the hang of environments now. Just checking our numbers
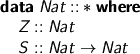
and finite sets, used as de Bruijn indices since last century.
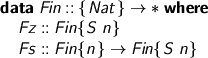
Well now, environments are an instance of :*:, the relational Kleene star. (Some people have started calling these ‘thrists’, but I don’t see why they need a new name.)
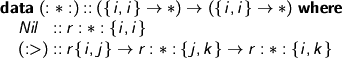
That’s to say, environments are made of little bits of environment extension:
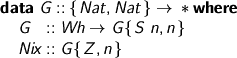
You can grow the context, but you can also Nix it, throwing away all the values. This type’s negotiable: as long as you can explain the action of each chunk.
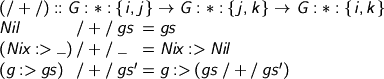
Let’s also make sure we can project. Of course, you know that if you have a variable in your hand, the corresponding environment can’t have been Nixed.
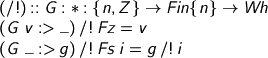
Let’s evaluate, given an environment that goes all the way down. For canonical stuff, we’re weak-head-normal already, so we just close up underneath the head constructor, stashing the (shared) environment.
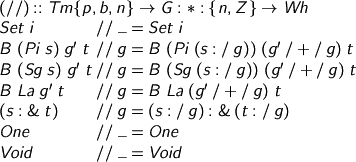
Otherwise, we might have some work to do. Bound vars, we fish from the environment; definitions, we expand; eliminations we must actually compute (see below). For closures, we unpack the stashed environment, stitch it into place, and carry on computing. Note that always the indexing keeps us honest: we can’t leave a de Bruijn variable dangling; we can’t unpack a closure and discard its environment because only that environment has the correct starting index to let us evaluate the term!
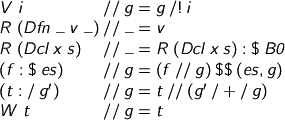
How to compute. One step goes like this. We provide an environment, because we haven’t evaluated the spine yet.
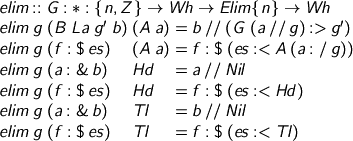
Careful with the β rule! We evaluate the argument a in its environment, then bung the result into the stashed environment, making it ready (at last!) to evaluate b. Try mixing the environments up or leaving them out and see if you can get past GHC.
Now, to do the whole spine, we need
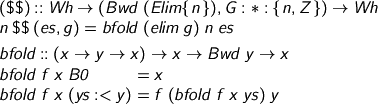
And that's us computing! When I get a moment, I'll show you my cheap trick (with coaching from Saizan) for writing
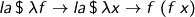
instead of
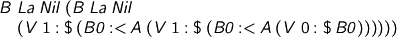
After that, I suppose I’d better show how to check types for these things, with an environment rather than substitutions all over the shop.
But it comes to this — a first-order representation of terms (so hole-filling does not require an expensive quotation process); weak-head-normal forms rather than full normalization; scope-safe environment management; the ability to insist on weak-head-normal form by type.