Time for the next episode…
M’colleague Bob Atkey once memorably described the capacity to put up with de Bruijn indices as a Cylon detector, the kind of reverse Turing Test that the humans in Battlestar Galactica invent, the better to recognize one another by their common inadequacies. He had a point.
In this post, I’ll discuss some of the issues which have driven us to a de Bruijn indexed representation of values, where once we used Haskell functions to model Epigram functions. I’ll also introduce some technology which will hopefully make the resulting representation accessible to non-Cylons. It’s made possible exactly because our de Bruijn terms have a type indexed by the number of variables in scope.
Remember, folks, in the twenty-first century, the point of types isn’t the crap you’re not allowed to write, it’s the other crap you don’t want to bother figuring out.
Back in the day, we would separate terms (first-order, with de Bruijn indices) from values (with a higher-order representation of binding). From a computational perspective, this was rather lovely: we could do functional programming with values, abstracting and applying them. A little extra effort was required to allow work with open terms, but this we could make systematic.
It used to go something like
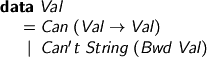
with application
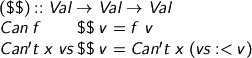
So although the free variables are Strings (and I'd usually cache the type, too), the bound variables live at the Haskell level. λf. λx. f (f x) becomes
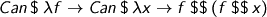
Implementing operators was really easy, because you could just pattern match on values — they were always computed to βδ-normal form.
Remark. Whilst this is a higher-order representation of values, it is not and should not be described as ‘higher-order abstract syntax’: on the one hand, free variables have a concrete first-order representation; on the other hand, the functions in Can are permitted to analyse and compute with their arguments by pattern matching on canonical value forms. Repeat. It is not HOAS. It is an untyped approximation to a Kripke-model construction, which morally goes by structural recursion on types.
Why ever did we want to leave this paradise? Well, we needed to do stuff like updating free variables (standing for holes), involving traversal of the syntax tree. The higher order structure doesn’t help, especially as references to things to update might readily lurk inaccessibly within a Haskell closure. To update a value, we’d quote it to a term, traverse the term, then reevaluate. Expensive. Worse, we’d often have to compute the β-normal forms of proofs to get a term out, even though we have proof irrelevance.
So, first-order it is, and for age old reasons, named free references (R) and de Bruijn indices for bound variables (V) are the best bet. No α-conversion worries, and cheap replacement of bound variables with V-closed terms as James McKinna and Randy Pollack taught us.
For ease of typechecking, I want to make sure I check only β-normal forms (applied definitions are ok, as they carry a type, but λ is unlabelled). I use a spine representation: a term is either built by a canonical typecheckable constructor, or it is a variable with a spine of eliminators, and its type can be inferred. Typechecking is easy (see next time) and there’s constant time access to the head (which will turn out to be useful), but writing terms is ugly. Ugly like
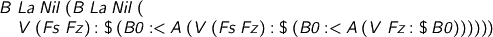
Not only de Bruijn indices, but also spine artefacts and application (A) eliminators (to be different from projections and whatever else we end up with). Hard to read and write, for non-Cylons.
Which brings me to the point of this post. It ought to be possible to write some sort of binder with a name and get the corresponding de Bruijn term computed for me. I don't want to write a higher-order term and quote it, because that takes a name supply. I had a secret SHE-hack which added de Bruijn sugar, but it was rather grim. Can't I find a way to use Haskell's λ like I did before? Well, now that Terms are indexed by the number of de Bruijn indices available, yes I can. Enter ad hoc polymorphism. I did an Agda experiment, then with quite a bit of help from Saizan on #epigram, I persuaded Haskell to eat it.
Step one, define less-or-equal for type-level natural numbers, inducing an injection on the corresponding finite sets.
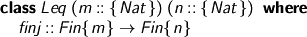
Remember, our de Bruijn indices live in finite sets.
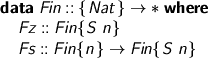
We’ll need these (overlapping, undecidable) instances.
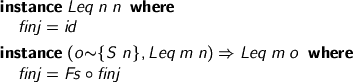
See? In each case, finj is the injection which shifts the de Bruijn indices when we move to the larger scope. You may wonder why that constraint is in the second rule. Why isn’t it just
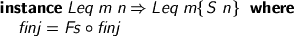
? I wish I knew. Overlapping instances objects to the latter, but allows the former. I suppose it’s clear that instance head Leq n n is strictly more specific than the instance head Leq m o, so it’s somehow unambiguous what is intended. Remember, the constraints are applied after the instance has been selected, rather than as preconditions to its selection.
Step 2. Try to bind something which picks the right index.
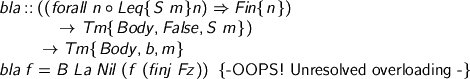
That doesn't work: the annoying but reasonable problem is that there is no reason why the Fz I wrote there should be the Fz that's finj-able from Fin {S m}. It could be any old Fz. In Agda, I could just be clear which Fz I want, but GHC won't let you tell it stuff like that: it insists that you make up a jolly little guessing game. Have it your way, GHC. Any time I'm making a term, I should be able to cough out the next Fz, autophlegmatically.
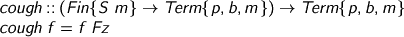
And now we’re in business.
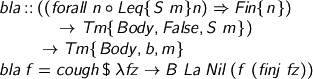
We can now write…
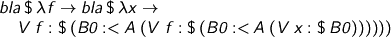
...and we've got rid of the numbers. Instead, we write Haskell λ abstractions which hand us polymorphic elements of any large enough variable set. Instance inference uses type information to figure out the right finj to get the number we need.
But it's still ugly. I want rid of all the spiny cruft. I'm already overloading the scope index of the variable representative, why doesn't an old faker like me overload its arity, too? In for a penny, in for a pound...
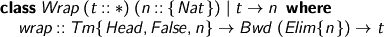
When will a type t wrap a level n head-and-spine? Well, level n terms will do that! Note the careful fundep: I’ll need t to determine n, because t will turn out to be the type at which we use a variable, and we will still need to know how much to finj it.
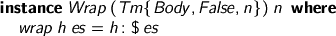
So will a function from terms, if you feed it a term.
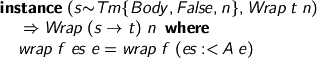
Again, the instance fires if we want a function, then the constraint fixes the domain.
So now it's finj-and-wrap time!
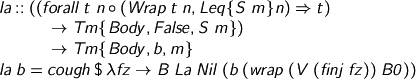
The polymorphic function we hand to the binder body is now ready to eat some arguments and make a spine from them, with the correctly indexed variable at its head. We can now write:
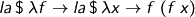
I’ve also chucked in Π and Σ variants.
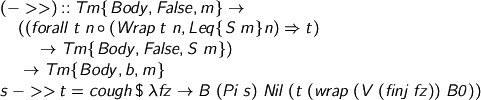
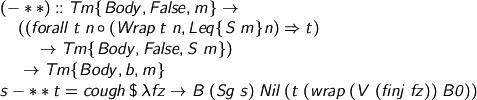
So, for example, the type of the polymorphic identity function
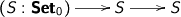 becomes
becomes
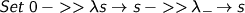
So, everything’s first order, but we’ve half a chance of seeing what we’re doing.